According to managerial economics, individuals have different risk preferences that they take into consideration when deciding whether to purchase a product. Different risk preferences result from differences in individual satisfaction or dissatisfaction arising from risk.
Utility is a subjective measure of satisfaction that’s unique to an individual. A utility function is an index or scale that measures the relative utility of various outcomes. Economists use utils to measure the amount of an individual’s satisfaction. The concept of utility enables individual risk preferences to be incorporated in decision-making criteria.
How to construct a utility function
Because utility is subjective, one individual’s utility function can’t be compared to another individual’s utility function. You must construct a utility function by determining the individual’s utility associated with each possible outcome.
To construct a utility function, you need to compare two alternatives. One alternative is called the standard lottery. The standard lottery has two possible outcomes, such as a payoff of $A occurring with probability P and a payoff of $B occurring with probability 1 – P. The second alternative is called the certainty equivalent. This alternative has a certain payoff of $C.
You’re indifferent when the expected utility from the certainty equivalent (first alternative) equals the expected utility from the standard lottery (second alternative). Mathematically, an individual is indifferent if
where U($) represents the utility associated with that payoff and P and (1 – P) represent probabilities.
Take the following steps to construct a utility function:
Assign utility values to two outcomes.
For example, receiving $0 may have a utility value of 0, while receiving $100 has a utility value of 200.
Define the monetary certainty equivalent.
Assume the two outcomes specified in Step 1 represent a standard lottery, where each outcome has a 50 percent chance of occurring. After you specify the standard lottery, you must determine what amount of money received with certainty would make you indifferent to the standard lottery. For example, you may decide that you’d be indifferent between receiving $45 for certain and taking the gamble represented by the standard lottery.
Determine the utility of the certainty equivalent.

Thus, you get 100 utils of satisfaction from $45.
Repeat these calculations for other standard lottery and certainty equivalent combinations to lead to other utilities.
For example, the new standard lottery has two possible outcomes: receive $0 or $45. Each outcome has a 50 percent chance of occurring. You decide that you’d be indifferent between receiving $25 for certain and taking the gamble represented by the standard lottery.

You get 50 utils of satisfaction from $25.
How risk attitudes effect buying behavior
Attitudes toward risk vary among individuals. Individual attitudes toward risk are grouped into the following three categories:
You’re risk adverse if you have two alternatives with the same expected monetary value, and you choose the alternative with less variation in outcomes.
You’re risk neutral if you have two alternatives with different variations in outcomes and the same expected monetary value and you’re indifferent between those alternatives. Risk neutral individuals aren’t influenced positively or negatively by risk. Risk neutral individuals will always choose the alternative with the highest expected value.
You’re a risk taker or risk lover if two alternatives have the same expected monetary value and you choose the one with the highest variability. Lottery players are risk takers.
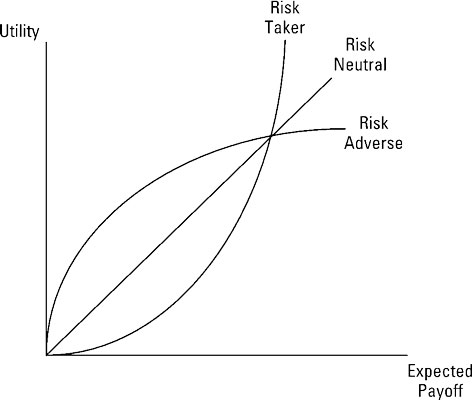
The illustration shows the relationship between the expected payoff and utility for individuals with different risk preferences. Note that the additional satisfaction risk adverse individuals get from higher payoffs is decreasing while the additional satisfaction risk takers get from higher payoffs is increasing.
How to use the expected utility criterion
After you determine the utilities, you maximize a decision’s expected utility. Expected utility equals the sum of each possible outcome’s utility multiplied by the probability of the outcome occurring.
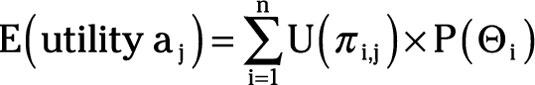
where the expected utility of action aj, E(utility aj), equals the summation for all states of nature of the utility associated with the payoff corresponding to action aj and state of nature èi, U(ðij), multiplied by the probability of state of nature èi occurring, P(èi).
After calculating the expected utility, the decision-maker chooses the action with the highest expected utility.
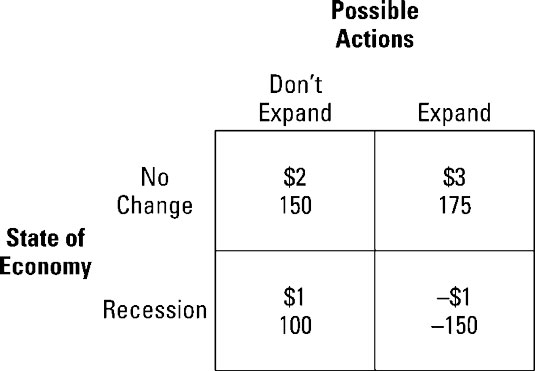
You want to determine whether to expand your business or maintain its current size. The resulting payoff depends on the action you take and whether or not the economy goes into a recession. The illustration shows the resulting payoff matrix with annual profit in millions of dollars.
In addition, the payoff matrix includes the utility you associate with each payoff. To use the expected utility criterion, you first determine the probability associated with each state of nature — what happens to the economy. You currently believe the probability that the economy experiences no change is 0.6 and the probability that the economy goes into recession is 0.4.
To determine which action to take based upon the expected utility criterion, you take the following steps:
Calculate the expected utility for not expanding.
For each state of nature, multiply the probability of that state of nature by the payoff’s utility given that state of nature and not expanding. Add the resulting values to determine the expected utility.

Calculate the expected utility for expanding.

Choose the action with the highest expected utility.
You shouldn’t expand. The expected utility of not expanding is 130, which is higher than the expected utility of expanding, which is only 45.
Major advantages of the expected utility criterion include its incorporation of all possible outcomes and the probability of an outcome occurring. In addition, the reliance on utility enables you to incorporate risk preferences in the decision-making process.
The primary disadvantage associated with this criterion is its reliance on a subjective measure. Risk preferences and utility functions vary from individual to individual; therefore, it’s impossible to make comparisons between different people.






