So-called p-series are relatively simple but important series that you can use as benchmarks when determining the convergence or divergence of more complicated series. A p-series is of the form
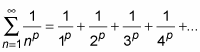
(where p is a positive power). The p-series for p = 1 is called the harmonic series. Here it is:
Although this grows very slowly — after 10,000 terms, the sum is only about 9.79! — the harmonic series in fact diverges to infinity.
By the way, this is called a harmonic series because the numbers in the series have something to do with the way a musical string like a guitar string vibrates — don’t ask. For history buffs, in the 6th century b.c., Pythagoras investigated the harmonic series and its connection to the musical notes of the lyre.
Here’s the convergence/divergence rule for p-series:
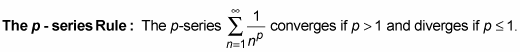
As you can see from this rule, the harmonic series forms the convergence/divergence borderline for p-series. Any p-series with terms larger than the terms of the harmonic series diverges, and any p-series with terms smaller than the terms of the harmonic series converges.
The p-series for p = 2 is another common one:
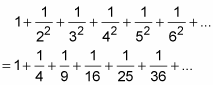
The p-series rule tells you that this series converges. It can be shown that the sum converges to
But, unlike with the geometric series rule, the p-series rule only tells you whether or not a series converges, not what number it converges to.






