Thomas Edison, who invented the light bulb and thus proved that he had some serious brain power, once said, “We don’t know a millionth of one percent about anything.” Edison may have been right when it comes to knowledge in general, but when you take the PSAT/NMSQT, you can easily find the right answer to 100% of the questions involving percents.
A percent is nothing more than a useful way to represent how much of 100 you’re talking about. Because 100% of anything is the whole thing, 50% is half, 25% is a quarter, and so forth. You see percents expressed with the word of, as in 66% of. The of is a stand-in for multiplication. Here’s how to approach percent problems:
Use your calculator if it has a % button. Some do; some don’t. If you have a % button on your calculator and you need to find 13% of 189, you can simply enter “13% x 189” to see that the answer is 24.57.
No percent button? Just convert the percent to a decimal by moving the decimal point two spaces to the left. In that case you’d enter “0.13 x 189” for the same result. You can also change a percent to a fraction (13% = 13/100).
Consider plugging in. This PSAT/NMSQT trick, plugging in, is tailor-made for percent problems. Plug in 100 and you’re all set.
Remember the “is-of” formula. In this formula, you have
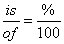
so if you’re asked, “80% of what number is 8,” you can see that
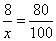
Now cross multiply: 80x = 800. Divide by 80 and you get x = 10.
Pay special attention to problems asking for the percent of increase or decrease. Plugging in helps here also, or you can use this formula:
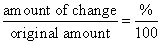
Don’t forget that percentages may be more than 100. You’d probably like your allowance to increase by 300% (so you’d pocket 4 times as much money), but it’s more likely that your college tuition will rise 500% by the time you graduate.
Ready for some percent problems? Give these your best shot.
Jane goes to get her hair cut and tells the person cutting her hair that she would like her hair to be 25% shorter than it currently is. After the haircut, Jane’s hair is 12 inches long. How many inches long was Jane’s hair before the haircut?
(A) 9
(B) 12
(C) 14
(D) 16
(E) 18
A bookstore sells books for 20% more than it buys them for. During a sale, a customer buys a book with a 25% discount coupon. What percent of the price that the store paid did the book sell for?
(A) 60%
(B) 75%
(C) 90%
(D) 100%
(E) 110%
Forty percent of the seats at a baseball stadium are in the shade at 4 p.m. If the stadium has 25,000 seats, how many seats are in the sun at 4 p.m.?
(A) 5,000
(B) 10,000
(C) 12,500
(D) 15,000
(E) 20,000
Now check your answers:
D. 16
Plugging in is a great strategy for solving this problem. If Jane began with 14 inches of hair — Choice (C) — then after the haircut she’ll still have 75% of that length: 14(0.75) = 10.5 inches. Jane has more hair left than that, so pick a longer starting length.
If Jane began with 16 inches of hair, Choice (D), then she’d have 16(0.75) = 12 inches of hair after the cut — the answer you’re looking for!
C. 90%
As usual, you want to use 100 as your initial amount in a percent problem, even if it sounds silly for a book to cost $100. That means that the customers saw the price as 20% or $20 higher: $120. A 25% discount is the same as paying 75% of the price, so the sale price is 120(0.75) = $90.
$90 is 90% of $100, so Choice (C) is the one you want.
D. 15,000
If 40% of the seats are in the shade, then 60% of them are in the sun. To find out how many seats are in the sun, you want to know what number is 60% of 25,000. Using the formula
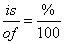
and letting x be the number you’re looking for:
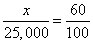
Cross-multiply and simplify, and you see that x = 15,000, Choice (D).

