The area function is a bit weird. Brace yourself. Say you’ve got any old function, f(t). Imagine that at some t-value, call it s, you draw a fixed vertical line. (Note that because this line is fixed, s is a constant, not a variable.) Check out the figure below.
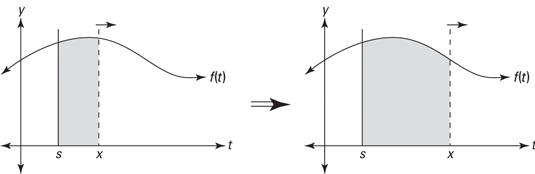
Then, you add a moveable vertical line (the dotted line in the figure) at the t-value x. You start with the dotted line at s (“s” is for starting point), and then drag it to the right. As you drag the line, you sweep out a larger and larger area under the curve between s and x. This area is a function of x, the position of the moving line.
In symbols, you write

The dt is a little increment along the t-axis — actually an infinitesimally small increment.
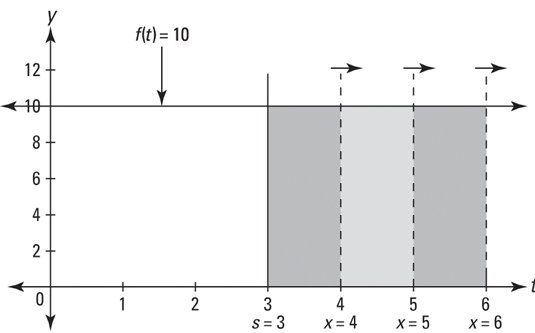
Here’s a simple example to make sure you’ve got a handle on how the area function works. By the way, don’t feel bad if you find this extremely hard to grasp — you’ve got lots of company. Say you’ve got the simple function f(t) = 10 — that’s a horizontal line at y = 10. If you sweep out area beginning at s = 3, you get the following area function:
You can see that the area swept out from 3 to 4 is 10 because, in dragging the line from 3 to 4, you sweep out a rectangle with a width of 1 and a height of 10, which has an area of 1 times 10, or 10. See the figure below.

Now, imagine that you drag the line across at a rate of one unit per second. You start at x = 3, and you hit 4 at 1 second, 5 at 2 seconds, 6 at 3 seconds, and so on. How much area are you sweeping out per second? Ten square units per second because each second you sweep out another 1-by-10 rectangle. Notice — this is huge — that because the width of each rectangle you sweep out is 1, the area of each rectangle — which is given by height times width — is the same as its height because anything times 1 equals itself. You’ll see why this is huge in a minute.
Okay, are you sitting down? You’ve reached one of the big Ah ha! moments in the history of mathematics. Recall that a derivative is a rate. So, because the rate at which the previous area function grows is 10 square units per second, you can say its derivative equals 10. Thus, you can write —

Now here’s the critical thing: Notice that this rate or derivative of 10 is the same as the height of the original function f(t) = 10 because as you go across 1 unit, you sweep out a rectangle that’s 1 by 10, which has an area of 10, the height of the function.
This works for any function, not just horizontal lines. The next figure shows the function g(t) and its area function
that sweeps out the area beginning at s = 2.
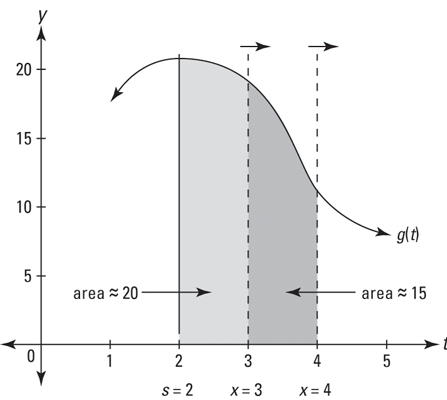
You can see that
equals roughly 20 because the area swept out between 2 and 3 has a width of 1 and the curved top of the “rectangle” has an average height of about 20. So, during this interval, the rate of growth of
is about 20 square units per second. Between 3 and 4, you sweep out about 15 square units of area because that’s roughly the average height of g(t) between 15 and 4. So, during the second number two — the interval from x = 3 to x = 4 — the rate of growth of
is about 15.
The rate of area being swept out under a curve by an area function at a given x-value is equal to the height of the curve at that x-value.
Although it’s a bit loose — in the discussion of the above figure — saying things like “roughly” this and “average” that, don’t worry; when you do the math, it all works out. The important thing to focus on is that the rate of area being swept out under a curve is the same as the height of the curve.

