In physics, when the net force acting on an object is elastic (such as on a vertical or horizontal spring), the object can undergo a simple oscillatory motion called simple harmonic motion.
An oscillatory motion is one that undergoes repeated cycles.
The force that tries to restore the object to its resting position is proportional to the displacement of the object. In other words, it obeys Hooke’s law.
Elastic forces suggest that the motion will just keep repeating (that isn’t really true, however; even objects on springs quiet down after a while as friction and heat loss in the spring take their toll). This section delves into simple harmonic motion and shows you how it relates to circular motion. Here, you graph motion with the sine wave and explore familiar concepts such as position, velocity, and acceleration.
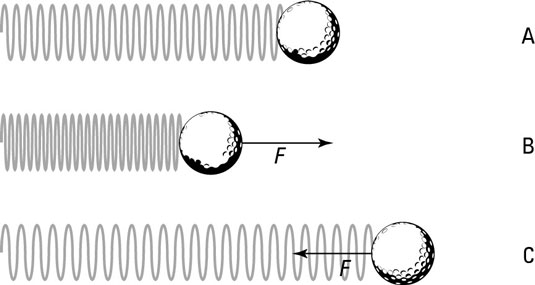
Take a look at the golf ball in the figure. The ball is attached to a spring on a frictionless horizontal surface. Say that you push the ball, compressing the spring, and then you let go; the ball shoots out, stretching the spring. After the stretch, the spring pulls back and once again passes the equilibrium point (where no force acts on the ball), shooting backward past it. This happens because the ball has momentum, and when the ball is moving, bringing it to a stop takes some force. Here are the various stages the ball goes through, matching the letters in the figure (and assuming no friction):
Point A. The ball is at equilibrium, and no force is acting on it. This point, where the spring isn’t stretched or compressed, is called the equilibrium point.
Point B. The ball pushes against the spring, and the spring retaliates with force F opposing that pushing.
Points B to C. The spring releases, and the ball springs to an equal distance on the other side of the equilibrium point. At this point, the ball isn’t moving, but a force acts on it, F, so it starts going back the other direction.
The ball passes through the equilibrium point on its way back to Point B. At the equilibrium point, the spring doesn’t exert any force on the ball, but the ball is traveling at its maximum speed. Here’s what happens when the golf ball bounces back and forth; you push the ball to Point B, and it goes through Point A, moves to Point C, shoots back to A, moves to B, and so on: B-A-C-A-B-A-C-A, and so on. Point A is the equilibrium point, and both Points B and C are equidistant from Point A.
What if the ball were to hang in the air on the end of a spring, as the second figure shows? In this case, the ball oscillates up and down. Like the ball on a surface in the first figure, the ball hanging on the end of a spring oscillates around the equilibrium position; this time, however, the equilibrium position isn’t the point where the spring isn’t stretched.
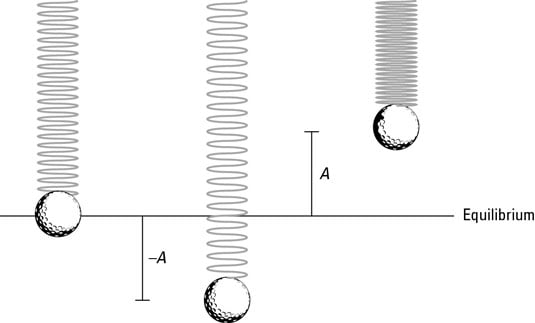
The equilibrium position is defined as the position at which no net force acts on the ball. In other words, the equilibrium position is the point where the ball can simply sit at rest. When the spring is vertical, the weight of the ball downward matches the pull of the spring upward. If the x position of the ball corresponds to the equilibrium point, xi, the weight of the ball, mg, must match the force exerted by the spring. Because F = kxi, you can write the following:
mg = kxi
Solving for xi gives you the distance the spring stretches because of the ball’s weight:
When you pull the ball down or lift it up and then let go, it oscillates around the equilibrium position, as the figure shows. If the spring is elastic, the ball undergoes simple harmonic motion vertically around the equilibrium position; the ball goes up a distance A and down a distance –A around that position (in real life, the ball would eventually come to rest at the equilibrium position, because a frictional force would dampen this motion).
The distance A, or how high the object springs up, is an important one when describing simple harmonic motion; it’s called the amplitude. The amplitude is simply the maximum extent of the oscillation, or the size of the oscillation.

