When you are working with potential barrier of height V0 and width a where E > V0, this means that the particle has enough energy to pass through the potential barrier and end up in the x > a region. This is what the Schrödinger equation looks like in this case:
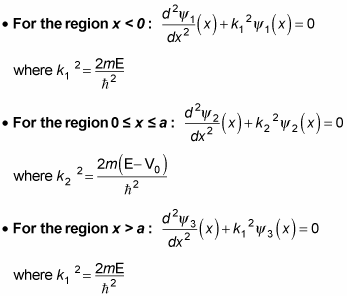
The solutions for
are the following:
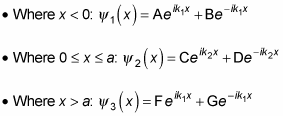
In fact, because there's no leftward traveling wave in the x > a region,
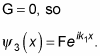
So how do you determine A, B, C, D, and F? You use the continuity conditions, which work out here to be the following:
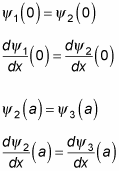
Okay, from these equations, you get the following:
A + B = C + D
ik1(A – B) = ik2(C – D)
Ceik2a + De–ik2a = Feik1a
ik2Ceik2a – ik2De–ik2a = ik1Feik1a
So putting all of these equations together, you get this for the coefficient F in terms of A:
Wow. So what's the transmission coefficient, T? Well, T is
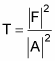
And this works out to be
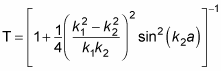
Whew! Note that as k1 goes to k2, T goes to 1, which is what you'd expect.
So how about R, the reflection coefficient? Without going into the algebra, here's what R equals:
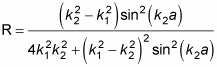
You can see what the E > V0 probability density,
looks like for the potential barrier in the figure.
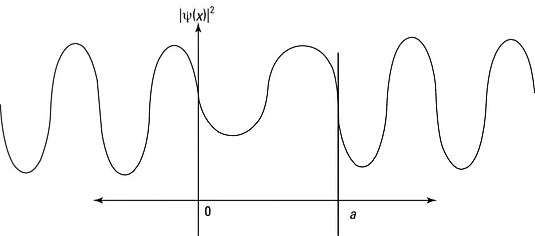
That completes the potential barrier when E > V0.






