You can use physics to calculate how friction affects rotational equilibrium. For example, say a hardware store owner comes to you for help with a problem. A clerk has climbed near the top of a ladder to hang a sign for the company’s upcoming sale. The owner doesn’t want the ladder to slip — lawsuits, he explains — so he asks you whether the ladder is going to fall.
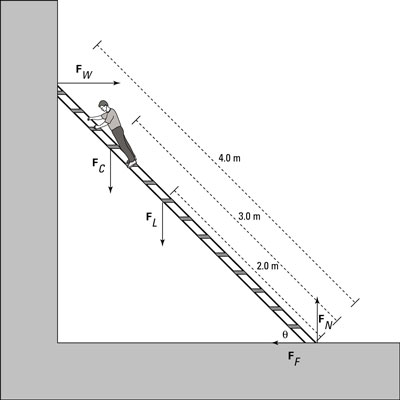
The situation appears in the figure. Here’s the question: Will the force of friction keep the ladder from moving if theta is 45 degrees and the static coefficient of friction with the floor is 0.7?
You have to work with net forces to determine the overall torque. Write down what you know (you can assume that the weight of the ladder is concentrated at its middle and that you can neglect the force of friction of the ladder against the wall because the wall is very smooth):
FW = Force exerted by the wall on the ladder
FC = Weight of the clerk = 450 N
FL = Weight of the ladder = 200 N
FF = Force of friction holding the ladder in place
FN = Normal force
You need to determine the needed force of friction here, and you want the ladder to be in both linear and rotational equilibrium. Linear equilibrium tells you that the force exerted by the wall on the ladder, FW, must be the same as the force of friction in magnitude but opposite in direction, because those are the only two horizontal forces. Therefore, if you can find FW, you know what the force of friction, FF, needs to be.
You know that the ladder is in rotational equilibrium, which means that
(where net torque is represented by the Greek letter tau.) To find FW, take a look at the torques around the bottom of the ladder, using that point as the pivot point. All the torques around the pivot point have to add up to zero. The direction of all the torque vectors is in the plane perpendicular to the plane of the figure, so consider only the component of these vectors in that direction (a positive component would correspond to a counterclockwise rotational force in the figure, and a negative component would correspond to a clockwise rotational force). Because you’re dealing with the components of the vector, which are numbers, you don’t write them in bold type.
Here’s how to find the three torques around the bottom of the ladder:
*Torque due to the force from the wall against the ladder. Here, r = 4.0 m is the full length of the ladder:

Note that the torque due to the force from the wall is negative because it tends to produce a clockwise motion.
Torque due to the clerk’s weight. In this case, r is 3.0 meters, the distance from the bottom of the ladder to the clerk’s location:

Torque due to the ladder’s weight. You can assume that the ladder’s weight is concentrated in the middle of the ladder, so r = 2.0 meters, half the total length of the ladder. Therefore, the torque due to the ladder’s weight is

These last two torques are positive because the forces generate a counterclockwise turning force, as the figure shows.
Now, because
you get the following result when you add all the torques together:

The force the wall exerts on the ladder is 437 newtons, which is also equal to the frictional force of the bottom of the ladder on the floor, because FW and the frictional force are the only two horizontal forces in the whole system. Therefore,
FF = 437 N
You know the force of friction that you need. But how much friction do you actually have? The basic equation for friction tells you that
where
is the coefficient of static friction and FN is the normal force of the floor pushing up on the ladder, which must balance all the downward-pointing forces in this problem because of linear equilibrium. This means that
FN = WC + WL = 450 N + 200 N = 650 N
Plugging this into the equation for FF actual and using the value of
gets you the following:
You need 437 newtons of force, and you actually have 455 newtons. Good news — the ladder isn’t going to slip.





