You know that pressure increases the farther you go underwater, but by how much? As a physicist, you can put some numbers in and get numerical results out. Just what pressure would you expect for a given depth?
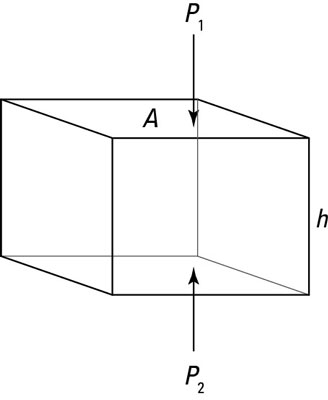
Say that you’re underwater and you’re considering the imaginary cube of water you see in the figure. At the top of the cube, the water pressure is P1. At the bottom of the cube, it’s P2. The cube has horizontal faces of area A and a height h. First, find the forces on the top and bottom of the cube.
The sum of the forces is the difference between the force on the bottom face of the cube, F2, and the force on the top face of the cube, F1:
You can say the force pushing down on the top face is F1 = P1A and that the force pushing on the bottom face is F2 = P2A. Therefore, in terms of pressure, the sum of forces is the following:
So what’s the net force upward on the cube of water? The upward force must be equal to the weight of the water, mg, where m is the mass of the water and g is the gravitational constant (9.8 meters/second2). So you have the following equation:
P2A – P1A = mg
Hmm. You don’t know m, the mass of the water. Can you get the weight of the water in terms of A, the area of the top and bottom faces of the cube? The mass of the water is the density of water,
multiplied by the volume of the cube, which is Ah. So you can replace m with
which gives you the following equation:
Now you’re talking. Dividing everything by A gives you the difference in pressures:
Keep in mind that if you call the difference in the pressures
you get the following equation:
The preceding equation is an important, general result that holds for any fluid: water, air, gasoline, and so on. This equation says that the difference in pressure between two points in a fluid is equal to the fluid’s density multiplied by g (the acceleration due to gravity) multiplied by the difference in height between the two points.
The following example shows you what the pressure formula looks like in practice.
How much does the pressure increase for every meter you go underwater? You know that
so plug in the numbers and do the math:
That works out to be about 1.4 pounds per square inch added pressure for every meter you go down.
If you were wondering how the units work out, rearrange the units from the first equation:
A kg∙m/s2 is just a newton, and a N/m2 is a pascal, so the units boil down to pascals:
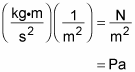
That’s a fair bit of added pressure. But what if you decided to take a dip in a pool of mercury instead (don’t try this at home)? Mercury has a density of 13,600 kg/m3, as opposed to water’s density at 1,000 kg/m3. In this case, the added pressure for every meter would be
That’s an increase of about 19 pounds per square inch for every meter you go down — and that’s a lot of pressure.
So does that mean that the pressure 1 meter under the surface of a pool of mercury is about 19 pounds per square inch? No, because you have to add to that pressure the pressure of the air on top of it, so you have the following:
Pt = Pm + Pa
where Pt is the total pressure, Pm is the pressure due to the mercury, and Pa is the pressure due to the air. To find the total pressure on something submerged in a liquid, you have to add the pressure due to the liquid to the atmospheric pressure, which is about 14.7 pounds per square inch, or 1.013 × 105 pascals.






