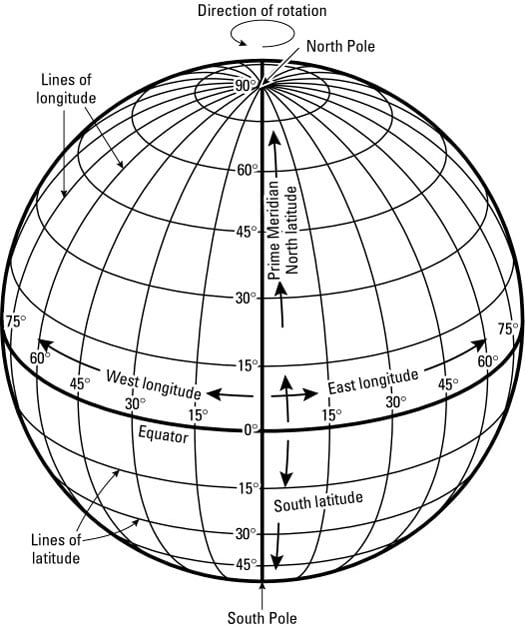
In geography, the world as a whole possesses a grid whose coordinates may be used to identify the absolute location of things. Indeed, that is why a Greek named Hipparchus invented the global grid some 2,200 years ago.
As chief librarian at the great library in Alexandria, Egypt, Hipparchus compiled information about lands and cities all over the expanding Greek world. He saw the value of accurately locating objects on a map, but in those days that was easier said than done. Maps were notoriously inaccurate, due in good measure to lack of a systematic means of stating the location of things. So Hipparchus set out to rectify the situation and came up with the global grid that is still in use today (see Figure 1).
Avoiding gridlock
Proper use of a grid coordinate system to state the absolute locations of things depends on a handful of prerequisites. Think of these as ways of avoiding gridlock:
- Familiarity breeds success. Knowledge of the naming and numbering of grid components is essential. If, for example, a stranger is not familiar with a city map, then telling her the hospital is at "the intersection of South 1st Street and West 1st Avenue" would have made no sense whatsoever. The same is true with respect to the global grid. That is, knowing how the lines are named and numbered is essential if you are to use the grid successfully.
- Unique components. Each line on the global grid must have a unique name. In a city map, for example, there must be only one road named South 1st Street, and only one named East 1st Avenue. If multiples exist, then more than one site could satisfy "the intersection of South 1st Street and East 1st Avenue." And that would rather defeat the concept of absolute location.
- No double-crossing allowed. Don't take that as a threat or accusation. What it means is that two lines on the global grid may cross each other only once. If they have multiple junctions then, such as the last point, there would be two or more intersections of, say, South 1st Street and East 1st Avenue.And again, that would defeat the concept of absolute location.
- Full names, please. You must use the full name of each line on the global grid. Again, the absolute location of the hospital is the intersection of South 1st Street and West 1st Avenue. Now suppose you had told that stranger, "The hospital's at the corner of 1st Street and 1st Avenue." Well, there may be several 1st Streets and 1st Avenues (South, North, East, West, what have you), so you may have several instances where a 1st Street crosses a 1st Avenue. Obviously, the potential for location confusion here defeats the purpose of absolute location. The remedy is to use the full name of each grid component.
The naming game
The global grid consists of imaginary lines of latitude and longitude (see Figure 1). Latitude lines go across the map — latitude comes from the Latin latitudo, meaning breadth, or the measure of the side-to-side dimension of a solid. Longitude lines run from top to bottom — longitude comes from the Latin longitudo, meaning length. This makes sense because when viewed on a globe, lines of longitude are generally lengthier than lines of latitude.
The global grid contains a principal line of latitude (the equator) and a principal line of longitude (the prime meridian). All other lines of latitude and longitude are named and numbered respectively from these starting lines. It makes sense, therefore, that if you want to make like Hipparchus and draw a grid on a globe, then these are the first two lines you would draw. But where would you put them, and why?
The equator
Because Earth is sphere-like, no compelling locale cries out and says, "Use me to locate the equator!" So where to put it? Old Hipparchus might simply have said, "It's Greek to me!" and placed it anywhere. Instead, he wrestled with the challenge and came up with an ingenious solution.
He knew that the Earth is sphere-like and that it rotates on an imaginary line called the axis. Look on a globe and you find two fixed points, halfway around the earth from each other, where the axis intersects the Earth's surface: the North Pole and the South Pole. So Hipparchus drew a line that ran all the way around the globe and was always an equal distance (hence, equator) from the two Poles. The result is a latitudinal "starting line" from which all others could be placed on the globe.
The prime meridian
The longitudinal "starting line" is called the prime meridian, which signifies its importance as the line from which all other lines of longitude are numbered. Locating this line proved more problematical than locating the equator. Quite simply, no logical equivalent of the equator exists with respect to longitude. Thus, while the equator came into general use as the latitudinal starting line, mapmakers were perfectly free to draw the longitudinal starting line anywhere they pleased. And that is what they did.
Typically, mapmakers drew the prime meridian right through their country's capital city. By the late 1800s, lack of a universal prime meridian had become a real pain in the compass. International trade and commerce were growing. Countries were claiming territory that would become colonial empires. But one country's world maps did not agree with another's, and the international climate made it increasingly advisable that they do so.
As a result, in 1884 the International Meridian Conference was convened in Washington, D.C., to promote the adoption of a common prime meridian. Out of that was born an agreement to adopt the British system of longitude as the world standard. Thus, the global grid's prime meridian passes right through the Royal Greenwich Observatory, which is in the London suburb of Greenwich, as well as parts of Europe, Africa, and the Atlantic Ocean. The British system was chosen largely because in 1884 Britain was the world's major military and economic power, and also had a fine tradition of mapmaking.

