All statistical tests are derived on the basis of some assumptions about your data, and most of the classical significance tests (such as Student t tests, analysis of variance, and regression tests) assume that your data is distributed according to some classical frequency distribution (most commonly the normal distribution).
Because the classic distribution functions are all written as mathematical expressions involving parameters (like means and standard deviation), they're called parametric distribution functions, and tests that assume your data conforms to a parametric distribution function are called parametric tests. Because the normal distribution is the most common statistical distribution, the term parametric test is most often used to mean a test that assumes normally distributed data.
But sometimes your data isn't parametric. For example, you may not want to assume that your data is normally distributed because it may be very noticeably skewed, as shown in part a of the figure.
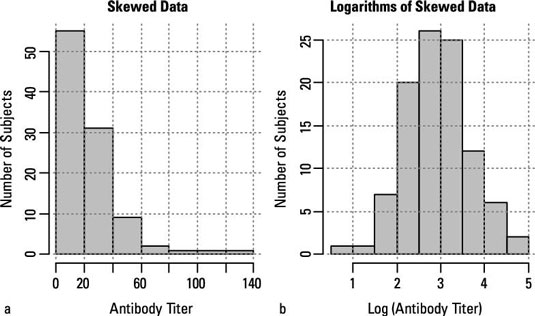
Sometimes, you may be able to perform some kind of transformation of your data to make it more normally distributed. For example, many variables that have a skewed distribution can be turned into normally distributed numbers by taking logarithms, as shown in part b. If, by trial and error, you can find some kind of transformation that normalizes your data, you can run the classical tests on the transformed data.
But sometimes your data is stubbornly abnormal, and you can't use the parametric tests. Fortunately, statisticians have developed special tests that don't assume normally distributed data; these are (not surprisingly) called nonparametric tests. Most of the common classic parametric tests have nonparametric counterparts.
As you may expect, the most widely known and commonly used nonparametric tests are those that correspond to the most widely known and commonly used classical tests.
| Classic Parametric Test | Nonparametric Equivalent |
|---|---|
| One-group or paired Student t test | Sign test; Wilcoxon signed-ranks test |
| Two-group Student t test | Wilcoxon sum-of-ranks test; Mann-Whitney U test |
| One-way ANOVA | Kruskal-Wallis test |
| Pearson Correlation test | Spearman Rank Correlation test |
Most nonparametric tests involve first sorting your data values, from lowest to highest, and recording the rank of each measurement (the lowest value has a rank of 1, the next highest value a rank of 2, and so on). All subsequent calculations are done with these ranks rather than with the actual data values.
Although nonparametric tests don't assume normality, they do make certain assumptions about your data. For example, many nonparametric tests assume that you don't have any tied values in your data set (in other words, no two subjects have exactly the same values). Most parametric tests incorporate adjustments for the presence of ties, but this weakens the test and makes the results nonexact.
Even in descriptive statistics, the common parameters have nonparametric counterparts. Although means and standard deviations can be calculated for any set of numbers, they're most useful for summarizing data when the numbers are normally distributed. When you don't know how the numbers are distributed, medians and quartiles are much more useful as measures of central tendency and dispersion.






