Sometimes the function that you’re trying to integrate is the product of two functions — for example, sin3 x and cos x. This would be simple to differentiate with the Product Rule, but integration doesn’t have a Product Rule. Fortunately, variable substitution comes to the rescue.
Given the example,
follow these steps:
Declare a variable as follows and substitute it into the integral:
Let u = sin x
You can substitute this variable into the expression that you want to integrate as follows:
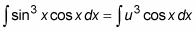
Notice that the expression cos x dx still remains and needs to be expressed in terms of u.
Differentiate the function u = sin x.
This gives you the differential du = cos x dx.
Substitute du for cos x dx in the integral:
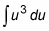
Now you have an expression that you can integrate:
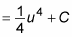
Substitute sin x for u:
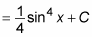
Now check this answer by differentiating with the Chain Rule:
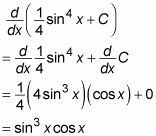
This derivative matches the original function, so the integration is correct.

