You can use physics to determine the force of gravity on an object that moves along an inclined plane. You can break the weight of the object down into components that are parallel to and perpendicular to the plane. The component perpendicular to the plane presses the object into the surface of the plane. The component of the weight that acts along the plane accelerates the object down the plane. Here you will find the component of gravity acting along the plane when the vertical force due to gravity is Fg.
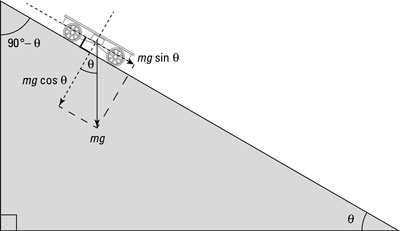
To work out the components of the weight parallel to and perpendicular to the inclined plane (the ramp in the figure), you need to know the relationship between the direction of the total weight and the direction of the ramp. The simplest way to determine this is to work out the angle between the weight and a line perpendicular to the ramp. This angle is labeled in the figure with the symbol for theta, which is equal to the angle of the ramp.
There are various ways you can use geometry to show that theta is equal to the angle of the ramp. For example, you may note that the angle between the weight and the line perpendicular to the ramp must be complementary to the angle at the top of the ramp, which is
Two angles are complementary if they add up to 90 degrees.
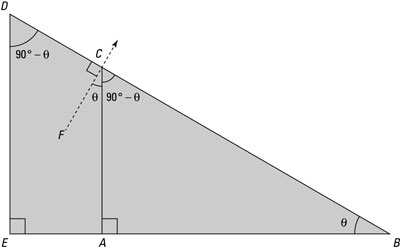
In this figure, the angle of the ramp is given by the angle ABC. The angle at the top of the ramp is the complement of this because the angles of a triangle add up to 180 degrees, so the angle
The angle BCA must be equal to the angle BDE because the triangles EBD and ABC are similar, so you can say that the angle
Finally, the angle BCA must be complementary to the angle ACF because they clearly add up to 90 degrees (along with right angle FCD, they form a straight line), so you finally have your answer:
If you use trigonometry to project the weight vector onto the lines perpendicular to and parallel to the ramp (refer to the first figure and rotate it by 30 degrees if doing so helps you see what’s going on), you obtain the expression for the component of the weight perpendicular to the ramp as this:
And the component of the weight that’s along the ramp is this:
Because you know the force, you can use Newton’s second law to work out the acceleration along the ramp:
At this point, you know that the acceleration of the cart along the ramp is given by
This equation holds for any object that gravity accelerates down a ramp, as long as friction doesn’t apply.






