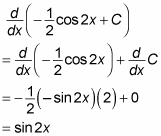Sometimes you need to integrate a function that is the composition of two functions — for example, the function 2x nested inside a sine function. If you were differentiating, you could use the Chain Rule. Unfortunately, no Chain Rule exists for integration.
Fortunately, a function such as
is a good candidate for variable substitution. Follow these steps:
Declare a new variable u as follows and substitute it into the integral:
Let u = 2x
Now substitute u for 2x as follows:

This may look like the answer to all your troubles, but you have one more problem to resolve. As it stands, the symbol dx tells you that the variable of integration is still x.
To integrate properly, you need to find a way to change dx to an expression containing du. That’s what Steps 2 and 3 are about.
Differentiate the function u = 2x.

Substitute 1/2du for dx into the integral:

You can treat the 1/2 just like any coefficient and use the Constant Multiple Rule to bring it outside the integral:

At this point, you have an expression that you know how to evaluate:

Now that the integration is done, the last step is to substitute 2x back in for u:

You can check this solution by differentiating using the Chain Rule: