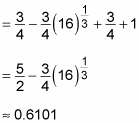To find an area between two functions, you need to set up an equation with a combination of definite integrals of both functions. For example, suppose that you want to calculate the shaded area between y = x2 and
as shown in this figure.
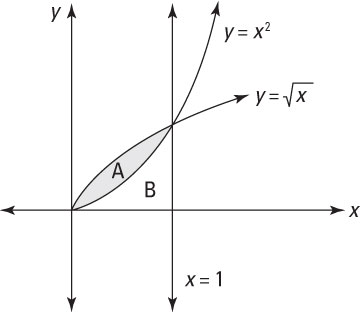
First, notice that the two functions y = x2 and
intersect where x = 1. This information is important because it enables you to set up two definite integrals to help you find region A:
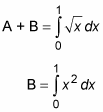
Although neither equation gives you the exact information that you’re looking for, together they help you out. Just subtract the second equation from the first as follows:
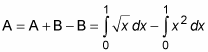
With the problem set up properly, now all you have to do is evaluate the two integrals:
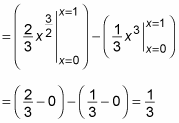
So the area between the two curves is
As another example, suppose that you want to find the area between y = x and
as shown in this figure.
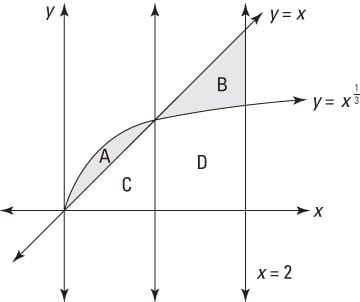
This time, the shaded area is two separate regions, labeled A and B. Region A is bounded above by
and bounded below by y = x. However, for region B, the situation is reversed, and the region is bounded above by y = x and bounded below by
Regions C and D are also labeled, as they both figure into the problem.
The first important step is finding where the two functions intersect — that is, where the following equation is true:
Fortunately, it’s easy to see that x = 1 satisfies this equation.
Now you want to build a few definite integrals to help you find the areas of region A and region B. Here are two that can help with region A:
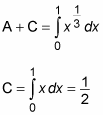
Notice that the second definite integral is evaluated without calculus, using simple geometry. This is perfectly valid and a great timesaver.
Subtracting the second equation from the first provides an equation for the area of region A:
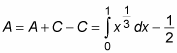
Now build two definite integrals to help you find the area of region B:
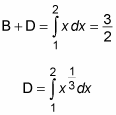
This time, the first definite integral is evaluated by using geometry instead of calculus. Subtracting the second equation from the first gives an equation for the area of region B:
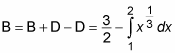
Now you can set up an equation to solve the problem:
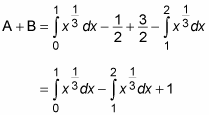
At this point, you’re forced to do some calculus:
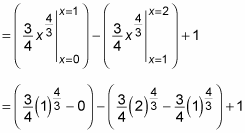
The rest is just arithmetic: