The opposite-angle identities change trigonometry functions of negative angles to functions of positive angles. Negative angles are great for describing a situation, but they aren’t really handy when it comes to sticking them in a trig function and calculating that value. So, for example, you can rewrite the sine of –30 degrees as the sine of 30 degrees by putting a negative sign in front of the function:
The identity works differently for different functions, though. First, consider the identities, and then find out how they came to be.
The opposite-angle identities for the three most basic functions are
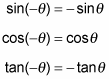
The rule for the sine and tangent of a negative angle almost seems intuitive. But what’s with the cosine? How can the cosine of a negative angle be the same as the cosine of the corresponding positive angle? Here’s how it works.
The functions of angles with their terminal sides in the different quadrants have varying signs. Sine, for example, is positive when the angle’s terminal side lies in the first and second quadrants, whereas cosine is positive in the first and fourth quadrants. In addition, positive angles go counterclockwise from the positive x-axis, and negative angles go clockwise.
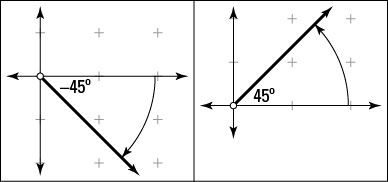
With those points in mind, take a look at the preceding figure, which shows a –45-degree angle and a 45-degree angle.
First, consider the –45-degree angle. This angle has its terminal side in the fourth quadrant, so its sine is negative. A 45-degree angle, on the other hand, has a positive sine, so
In plain English, the sine of a negative angle is the opposite value of that of the positive angle with the same measure.
Now on to the cosine function. In light of the cosine’s sign with respect to the coordinate plane, you know that an angle of –45 degrees has a positive cosine. So does its counterpart, the angle of 45 degrees, which is why
So you see, the cosine of a negative angle is the same as that of the positive angle with the same measure.
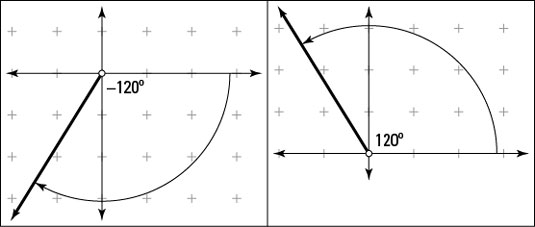
Next, try the identity on another angle, a negative angle with its terminal side in the third quadrant. The preceding figure shows a negative angle with the measure of –120 degrees and its corresponding positive angle, 120 degrees.
The angle of –120 degrees has its terminal side in the third quadrant, so both its sine and cosine are negative. Its counterpart, the angle measuring 120 degrees, has its terminal side in the second quadrant, where the sine is positive and the cosine is negative. So the sine of –120 degrees is the opposite of the sine of 120 degrees, and the cosine of –120 degrees is the same as the cosine of 120 degrees. In trig notation, it looks like this:
When you apply the opposite-angle identity to the tangent of a 120-degree angle (which comes out to be negative), you get that the opposite of a negative is a positive. Surprise, surprise. So, applying the identity, the opposite makes the tangent positive, which is what you get when you take the tangent of 120 degrees, where the terminal side is in the third quadrant and is therefore positive.






