If you want to find the approximate value of cos x, you start with a formula that expresses the value of sin x for all values of x as an infinite series. Differentiating both sides of this formula leads to a similar formula for cos x:
Now evaluate these derivatives:
Finally, simplify the result a bit:
As you can see, the result is a power series. Here’s how you write it by using sigma notation:
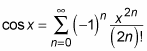
To gain some confidence that this series really works as advertised, note that the substitution x = 0 provides the correct equation cos 0 = 1. Furthermore, substituting x = 1 into the first four terms gives you the following approximation:
This estimate is accurate to four decimal places.






