Expressing and Approximating Functions Using the Taylor Series

It’s important to understand the difference between expressing a function as an infinite series and approximating a function by using a finite number of terms of series. You can think of a power series as a polynomial with infinitely many terms (Taylor polynomial).

Every Taylor series provides the exact value of a function for all values of x where that series converges. That is, for any value of x on its interval of convergence, a Taylor series converges to f(x).

Here’s the Taylor series in all its glory:

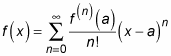
In practice, however, adding up an infinite number of terms simply isn’t possible. Nevertheless, you can approximate the value of f(x) by adding a finite number from the appropriate Taylor series.

An expression built from a finite number of terms of a Taylor series is called a Taylor polynomial, T_n(x). Like other polynomials, a Taylor polynomial is identified by its degree. For example, here’s the fifth-degree Taylor polynomial, T₅(x), that approximates e^x:

Generally speaking, a higher-degree polynomial results in a better approximation. For the value of e^x when x is near 100, you get a good estimate by using a Taylor polynomial for e^x with a = 100:

To sum up, remember the following:

• A convergent Taylor series expresses the exact value of a function.

• A Taylor polynomial, T_n(x), from a convergent series approximates the value of a function.