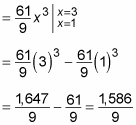Double integrals are usually definite integrals, so evaluating them results in a real number. Evaluating double integrals is similar to evaluating nested functions: You work from the inside out.
You can solve double integrals in two steps: First evaluate the inner integral, and then plug this solution into the outer integral and solve that. For example, suppose you want to integrate the following double integral:
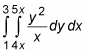
To start out, place the inner integral in parentheses so you can better see what you’re working with:
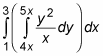
Now focus on what’s inside the parentheses. For the moment, you can ignore the rest. Your integration variable is y, so treat the variable x as if it were a constant, moving it outside the integral:
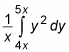
Notice that the limits of integration in this integral are functions of x. So the result of this definite integral will also be a function of x:
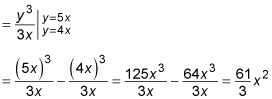
Now plug this expression into the outer integral. In other words, substitute it for what’s inside the parentheses:
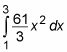
Evaluate this integral as usual: