The tangent and cotangent are related not only by the fact that they’re reciprocals, but also by the behavior of their ranges. In reference to the coordinate plane, tangent is y/x, and cotangent is x/y. The domains of both functions are restricted, because sometimes their ratios could have zeros in the denominator, but their ranges are infinite.
Domains of tangent and cotangent
Because x can’t equal 0 for the tangent function to work, this rule holds true: If
or any odd multiple of 90 degrees. In radians,
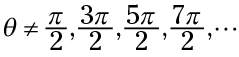
or any odd multiple of
Both the tangent and secant functions have ratios with x in the denominator, making their domains the same.
In order for the cotangent function to work, y can’t equal 0. If
or any multiple of 180 degrees. In radians,
or any multiple of π.
Ranges of tangent and cotangent
The ranges of both tangent and cotangent are infinite, which, when expressed in mathematical notation, looks like this:
The range values for these functions get very small (toward negative infinity) or very large (toward positive infinity) whenever the denominator of the respective ratio gets close to 0. When you divide some number by a very small value, such as 0.0001, the result is large. The smaller the denominator, the larger the result.





