The cosecant and secant functions are closely tied to sine and cosine, because they're the respective reciprocals. In reference to the coordinate plane, cosecant is r/y, and secant is r/x. The value of r is the length of the hypotenuse of a right triangle — which is always positive and always greater than x and y.
The only problem that arises when computing these functions is when either x or y is 0 — when the terminal side of the angle is on an axis. A function with a 0 in the denominator creates a number or value that doesn't exist (in math speak, the result is undefined), so anytime x or y is 0, you don't get any output from the cosecant or secant functions.
The x is 0 when the terminal side is on the y-axis, and the y is 0 when the terminal side is on the x-axis.
Domains of cosecant and secant
The domains of cosecant and secant are restricted — you can only use the functions for angle measures with output numbers that exist.
Any time the terminal side of an angle lies along the x-axis (where y = 0), you can't perform the cosecant function on that angle. In trig speak, the rule looks like this in degrees: If
or any multiple of 180 degrees. In radians,
Anytime the terminal side of an angle lies along the y-axis (where x = 0), you can't perform the secant function on that angle. So, in trig speak, you'd say this: If
or any odd multiple of 90 degrees. In radians,
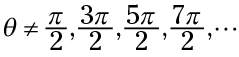
or any odd multiple of
Ranges of cosecant and secant
The ratios of the cosecant and secant functions on the coordinate plane, r/y and r/x, have the hypotenuse, r, in the numerator. Because r is always positive and greater than or equal to x and y, these fractions are always improper (greater than 1) or equal to 1. The ranges of these two functions never include proper fractions (numbers between –1 and 1).
If h(θ) and k(θ) are the output values of the functions





