The integral comparison test involves comparing the series you’re investigating to its companion improper integral. If the integral converges, your series converges; and if the integral diverges, so does your series.
Here’s an example. Determine the convergence or divergence of
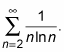
The direct comparison test doesn’t work because this series is smaller than the divergent harmonic series,
Trying the limit comparison test is the next natural choice, but it doesn’t work either — try it. But if you notice that the series is an expression you know how to integrate, you’re home free (you did notice that, right?). Just compute the companion improper integral with the same limits of integration as the index numbers of the summation — like this:
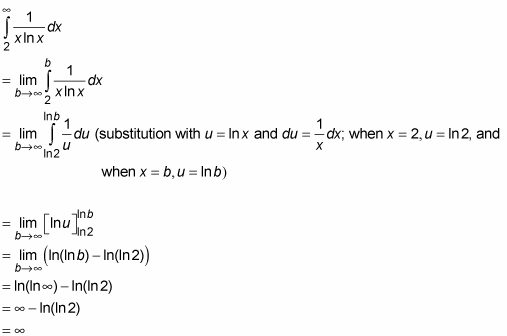
Because the integral diverges, the series diverges.
After you’ve determined the convergence or divergence of a series with the integral comparison test, you can then use that series as a benchmark for investigating other series with the direct comparison or limit comparison tests.
For instance, the integral test just told you that
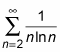
diverges. Now you can use this series to investigate
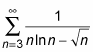
with the direct comparison test. Do you see why? Or you can investigate, say,
with the limit comparison test. Try it.
The integral comparison test is fairly easy to use, so don’t neglect to ask yourself whether you can integrate the series expression or something close to it. If you can, it’s a BINGO.
Here’s the mumbo jumbo for the integral comparison test. Note the fine print.
Integral Comparison Test: If f (x) is positive, continuous, and decreasing for all x ≥ 1 and if
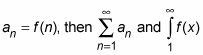
either both converge or both diverge.
Note that while this is the way that the Integral Comparison Test is usually stated, you can use any number you want for the lower limit of integration — like the way you used n = 2 in the above example.

