An object with uniform circular motion travels in a circle with a constant speed. Outside a physics class, practical examples may be hard to come by, unless you see a race car driver on a perfectly circular track with his accelerator stuck, a clock with a seconds hand that’s in constant motion, or the moon orbiting the Earth.
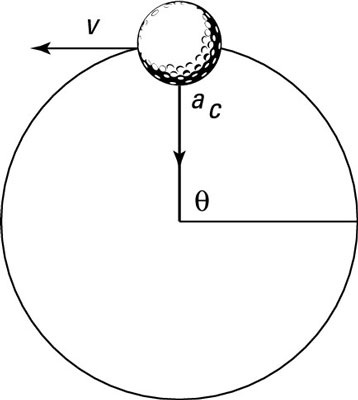
The figure shows another example, where a golf ball tied to a string is whipping around in circles. The golf ball is traveling at a uniform speed as it moves around in a circle, so you can say it’s traveling in uniform circular motion.
An object in uniform circular motion does not travel with a uniform velocity, because its direction changes all the time.
Any object that travels in uniform circular motion always takes the same amount of time to move completely around the circle. That time is called its period, designated by T.
If you’re swinging a golf ball around on a string at a constant speed, you can easily relate the ball’s speed to its period. You know that the distance the ball must travel each time around the circle equals the circumference of the circle, which is
(where r is the radius of the circle), so you can get the equation for finding an object’s period by first finding its speed:
Remember, if you solve for T, you get the equation for the period:
Say that you’re whirling a golf ball in a circle at the end of a 1.0-meter string every half-second. How fast is the ball moving? Time to plug in the numbers:
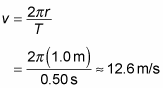
The ball moves with a linear speed of 12.6 meters/second. Just make sure you have a strong string!

