In physics, objects can have both linear and rotational kinetic energy. This can occur when an object rolls down a ramp instead of sliding, as some of its gravitational potential energy goes into its linear kinetic energy, and some of it goes into its rotational kinetic energy.
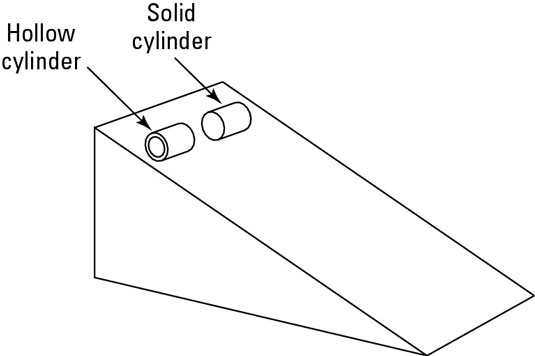
Look at the preceding figure, where you’re pitting a solid cylinder against a hollow cylinder in a race down the ramp. Each object has the same mass. Which cylinder is going to win? In other words, which cylinder will have the higher speed at the bottom of the ramp? When looking only at linear motion, you can handle a problem like this by setting the potential energy equal to the final kinetic energy (assuming no friction!) like this:

where m is the mass of the object, g is the acceleration due to gravity, and h is the height at the top of the ramp. This equation would let you solve for the final speed. Since the mass, m, cancels out from both sides of the equation, the final speed for linear motion without rotation is independent of mass.
But the cylinders are rolling in this case, which means that the initial gravitational potential energy becomes both linear kinetic energy and rotational kinetic energy. You can now write the equation as

You want to solve for v, so try grouping things together. You can factor (1/2)v2 out of the two terms on the right:
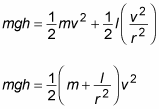
Isolating v, you get the following:
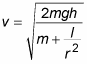
For the hollow cylinder, the moment of inertia equals mr2. For a solid cylinder, on the other hand, the moment of inertia equals (1/2)mr2. Substituting for I for the hollow cylinder gives you the hollow cylinder’s final velocity:
Substituting for I for the solid cylinder gives you the solid cylinder’s velocity:
Now the answer becomes clear.
1.15 times as fast, so the solid cylinder will win.
The hollow cylinder has as much mass concentrated at a large radius as the solid cylinder has distributed from the center all the way out to that radius, so this answer makes sense. With that large mass way out at the edge, the hollow cylinder doesn’t need to go as fast to have as much rotational kinetic energy as the solid cylinder. In fact, since the moment of inertia, I, always depends on the mass of the object, the mass term cancels out from top and bottom of our expression above for the final velocity of the object after it has rolled down the ramp. This means that the final velocity does not depend upon the mass at all, but only upon how that mass is distributed around the rotational axis. For all shapes that roll, can you guess which one would always win in a race where they roll down a ramp?

