Bisection and trisection involve cutting something into two or three equal parts. If you’re a fan of bicycles and tricycles and bifocals and trifocals — not to mention the biathlon and the triathlon, bifurcation and trifurcation, and bipartition and tripartition — you’re really going to love this discussion.
The main point here is that after you do the bisecting or trisecting, you end up with congruent parts of the segment or angle you cut up.
Segment bisection, the related term midpoint, and segment trisection are pretty simple ideas. (Their definitions, which follow, are used frequently in proofs.)
-
Segment bisection: A point, segment, ray, or line that divides a segment into two congruent segments bisects the segment.
-
Midpoint: The point where a segment is bisected is called the midpoint of the segment; the midpoint cuts the segment into two congruent parts.
-
Segment trisection: Two things (points, segments, rays, lines, or any combination of these) that divide a segment into three congruent segments trisect the segment. The points of trisection are called — check this out — the trisection points of the segment.
You shouldn’t have any trouble remembering the meanings of bisect and trisect, but here’s a mnemonic just in case: A bicycle has two wheels, and to bisect means to cut something into two congruent parts; a tricycle has three wheels, and to trisect means to cut something into three congruent parts.
Students often make the mistake of thinking that divide means to bisect, or cut exactly in half. This error is understandable because when you do ordinary division with numbers, you are, in a sense, dividing the larger number into equal parts
But in geometry, to divide something just means to cut it into parts of any size, equal or unequal. Bisect and trisect, of course, do mean to cut into exactly equal parts.
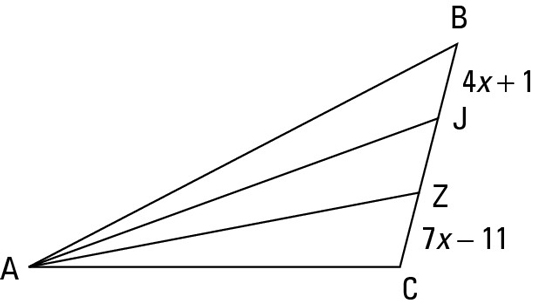
Here’s a problem you can try using the triangle in the above figure.
Okay, here’s how you solve it:
Just set these equal to each other and solve for x:
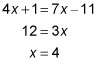
Plugging x = 4 into 4x + 1 and 7x – 11 gives you 17 for each segment. JZ must also be 17, so BC must total 3 times 17, or 51.
As it happens, this is never true.
If a side of a triangle is trisected by rays from the opposite vertex, the vertex angle can’t be trisected. The vertex angle often looks like it’s trisected, and it’s often divided into nearly equal parts, but it’s never an exact trisection.


