The Pythagorean identities are building blocks for many of the manipulations of trigonometric equations and expressions. They provide a greater number of methods for solving trig problems more efficiently, because they allow you to write complicated expressions in a much simpler form.
The Pythagorean identities are
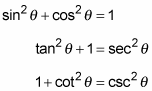
The notation in these identities is peculiar to trigonometry.
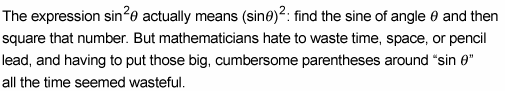
So they agreed on a condensed version: The superscript 2 right after “sin” means that you square the whole expression. The same type of notation also goes for the other functions.






