2023/2024 ASVAB For Dummies (+ 7 Practice Tests, Flashcards, & Videos Online)
Explore Book Buy On AmazonMake sure you know factors when you go to take the ASVAB. A factor is simply a number that is multiplied to get a product. Factoring a number means taking the number apart. It’s kind of like multiplying in reverse. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because all these numbers can be divided evenly into 12.
Here are some other factors:
2: 1, 2
3: 1, 3
4: 1, 2, 4
5: 1, 5
6: 1, 2, 3, 6
16: 1, 2, 4, 8, 16
20: 1, 2, 4, 5, 10, 20
45: 1, 3, 5, 9, 15, 45
Types of factors
A factor can be either a prime number or a composite number (except that 1 and 0 are neither prime nor composite). Prime numbers have only themselves and 1 as a factor, while composite numbers can be divided evenly by other numbers.
The prime numbers up to 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.
Prime factors
Any composite number can be written as a product of prime factors. Mathematicians call this process prime factorization. To find the prime factors of a number, you divide the number by the smallest possible prime number and work up the list of prime numbers until the result is itself a prime number.
Say you want to find the prime factors of 240. Because 240 is even, start by dividing it by the smallest prime number, which is 2: 240 ÷ 2 = 120. The number 120 is also even, so it can be divided by 2: 120 ÷ 2 = 60. Then 60 ÷ 2 = 30 and 30 ÷ 2 = 15.
Now, 15 isn’t even, so check to see whether you can divide it by 3 (the next highest prime number); 15 ÷ 3 = 5, which itself is a prime number, so 240 is now fully factored. Now, simply list the divisors to write the prime factors of 240:
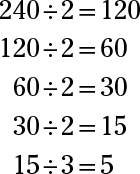
The prime factors of 240 are 2 × 2 × 2 × 2 × 3 × 5.

