In reality, multiple radio stations operate in the same metro area, or market. When you tune in a signal at 750 kHz, another signal may be at 760 kHz. To find out whether the adjacent signal impacts the simple receiver design, assume that the interference is a single tone, Aicos(2πfit). The received signal is now of the form
with fi assumed to lie just outside the +/– 5-kHz channel bandwidth centered on fc.
Using a generalized version of the phasor addition formula, you can show that the received envelope with single-tone interference is as follows:
Note that
The envelope detector recovers envelope R(t). To find R(t) for a new signal model, use the phasor additional formula, which can be shown to hold for time-varying amplitudes and phases of the constituent terms. The enhanced formula states that
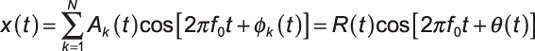
where
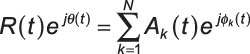
The key to this formula working is the common f0 found in each cosine term.
For AM plus single-tone interference, you can make the formula work by adding and subtracting fc in the interference term:
In the formula A1(t) = Ac[1 + am(t)],
Now, calculate
Add these complex numbers in rectangular form and then find the magnitude:
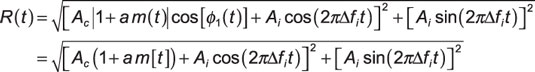
The last line follows from
Because
you can combine the terms and drop the absolute value. As a check, if Ai = 0, that is, no interference, the result for R(t) reduces to
The envelope detector is relatively easy to implement in hardware, but it’s a little difficult to analyze. You can explore the model for R(t) to get a feel for what’s going on. For starters, the input/output relationship is nonlinear, as evidenced by the squares and square root operations. Even with Ai = 0, R(t) contains an absolute value. At this point, assume m(t) = cos(2πfmt) as simple test case.
The Python function env_plot(t,Ac,Am,fm,Ai,fi) allows R(t) to be plotted as well as its spectrum. The spectrum PR(f) is a result of using PyLab’s psd() function.
In [<b>346</b>]: def env_plot(t,Ac,Am,fm,Ai,fi):
...: R = sqrt((Ac+Am*cos(2*pi*fm*t)
+Ai*cos(2*pi*dfi*t))**2
+(Ai*sin(2*pi*dfi*t))**2)
..: return R
In [<b>347</b>]: t = arange(0,20,1/500.) # T=20ms, fs=500 kHz
Exercise the function by using a time vector running over 20 ms at an effective sampling rate of 500 ksps and then plot time-domain and frequency-domain results side by side (see the 3 x 2 subplot array in the figure).
Set
Also set Am = 0.5, which is equivalent to setting a = 0.5 (50 percent modulation depth). The value of Ai steps over 0, 0.1, and 1.0. The 2-kHz message is within the 5-kHz message bandwidth requirement and
kHz for the interference places it in the adjacent channel (5 kHz is the crossover frequency).
Here are the primary IPython command line entries:
In [<b>447</b>]: R = env_plot(t,1,.5,2,0,7) In [<b>449</b>]: plot(t,R) In [<b>454</b>]: psd(R,2**13,500); In [<b>457</b>]: R = env_plot(t,1,.5,2,0.1,7) In [<b>459</b>]: plot(t,R) In [<b>464</b>]: psd(R,2**13,500); In [<b>467</b>]: R = env_plot(t,1,.5,2,1,7) In [<b>469</b>]: plot(t,R) In [<b>475</b>]: psd(R,2**13,500);
![[Credit: Illustration by Mark Wickert, PhD]](https://www.dummies.com/wp-content/uploads/379631.image14.jpg)
The only way to eliminate or reduce the interference is with a BPF in front of the envelope detector. The superheterodyne option is a good choice here, because the BPF doesn’t need to be tunable. At first, you may be disturbed that an out-of-band signal can produce in-band interference, but you should always expect the unexpected from nonlinearities. The upside is that the receiver design is still low cost.

