On the ACT Math test, you’ll probably have to multiply pairs of matrices that have either one row or one column. An easy way to multiply a vertical matrix by a horizontal matrix is to set up a small grid that resembles a multiplication table. This method allows you to fill in the numbers to get the right answer.
Matrix multiplication is not commutative, because the order in which you multiply two matrices can change the result. In other words, if P and Q are matrices, P multiplied by Q doesn’t necessarily equal Q multiplied by P.
Example
Here's an example of multiplying a vertical matrix by a horizontal matrix. If
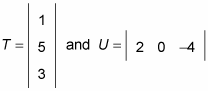
which of the following is the result when you multiply T by U?
Note that T has one column and U has one row, so you can multiply these two matrices in this order. So set up a grid with the first matrix in the left-hand column and the second matrix in the top row:

For each box in the grid, multiply the two numbers in the corresponding row and column, like this:

The contents of the grid is the result of the matrix multiplication:

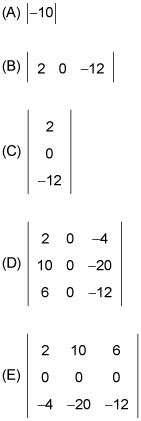
So the correct answer is Choice (D).






