A number system in algebra is a set of numbers — and different number systems are used to solve different types of algebra problems. Number systems include real numbers, natural numbers, whole numbers, integers, rational numbers, irrational numbers, even numbers, and odd numbers.
Real numbers: Real numbers comprise the full spectrum of numbers. They cover the gamut and can take on any form — fractions or whole numbers, decimal points or no decimal points. The full range of real numbers includes decimals that can go on forever. Real numbers are different from imaginary or complex numbers.
Natural numbers: A natural number is a number that comes naturally. What numbers did you first use? Remember someone asking, "How old are you?" You proudly held up four fingers and said, "Four!" Natural numbers are greater than zero but don't include fractions: 1, 2, 3, 4, 5, 6, 7, and so on, into infinity. You use natural numbers to count items and to make lists.
Whole numbers: Whole numbers are just all the natural numbers plus a zero: 0, 1, 2, 3, 4, 5, and so on, into infinity. They act like natural numbers and are used when whole amounts (no fractions) are required. Zero can also indicate none.
Algebraic problems often require you to round the answer to the nearest whole number. This makes perfect sense when the problem involves people, cars, animals, houses, or anything that shouldn't be cut into pieces.
Integers: Integers incorporate all the whole numbers and their opposites (or additive inverses of the whole numbers). Integers can be described as being positive and negative whole numbers and 0: . . . –3, –2, –1, 0, 1, 2, 3, . . . .
Integers are popular in algebra. When you solve a long, complicated problem and come up with an integer, you can be joyous because your answer is probably right. After all, it's not a fraction! This doesn't mean that answers in algebra can't be fractions or decimals. It's just that most textbooks and reference books try to stick with nice answers to increase the comfort level and avoid confusion.
Rational numbers: Rational numbers are numbers that act rationally! In this case, acting rationally means that the decimal equivalent of the rational number behaves. The decimal ends somewhere, or it has a repeating pattern to it. That's what constitutes "behaving." Some examples of rational numbers with decimals that terminate include 2, 3.4, 5.77623, and –4.5.
Some examples of rational numbers with decimals that repeat the same pattern include the following:
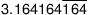
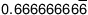
(The horizontal bar over the 164 and the 6 lets you know that these numbers repeat forever.) In all cases, rational numbers can be written as a fraction. They all have a fraction that they are equal to.
Irrational numbers: Irrational numbers are real numbers that are not rational numbers. An irrational number cannot be written as a fraction, and decimal values for irrationals never end and never have a nice pattern to them. For example, pi, with its never-ending decimal places, is irrational.
Imaginary/complex numbers: A number that isn't real can be imaginary or complex. An imaginary number contains some multiple of i, which is the following:
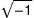
For example, 2 + 3i is a complex number.
Even numbers: An even number is one that divides evenly by 2, such as 2, 4, 18, and 352.
Odd numbers: An odd number is one that does not divide evenly by 2, such as 1, 3, 27, and 485.

