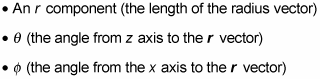In quantum physics, you sometimes need to use spherical coordinates instead of rectangular coordinates. For example, say you have a 3D box potential, and suppose that the potential well that the particle is trapped in looks like this, which is suited to working with rectangular coordinates:
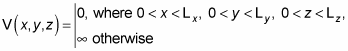
Because you can easily break this potential down in the x, y, and z directions, you can break the wave function down that way, too, as you see here:
Solving for the wave function gives you the following normalized result in rectangular coordinates:
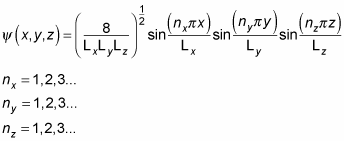
The energy levels also break down into separate contributions from all three rectangular axes:
E = Ex + Ey + Ez
And solving for E gives you this equation:
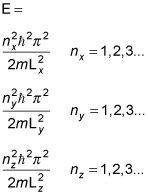
But what if the potential well a particle is trapped in has spherical symmetry, not rectangular? For example, what if the potential well were to look like this, where r is the radius of the particle's location with respect to the origin and where a is a constant?
Clearly, trying to stuff this kind of problem into a rectangular-coordinates kind of solution is only asking for trouble, because although you can do it, it involves lots of sines and cosines and results in a pretty complex solution. A much better tactic is to solve this kind of a problem in the natural coordinate system in which the potential is expressed: spherical coordinates.
The following figure shows the spherical coordinate system along with the corresponding rectangular coordinates, x, y, and z.
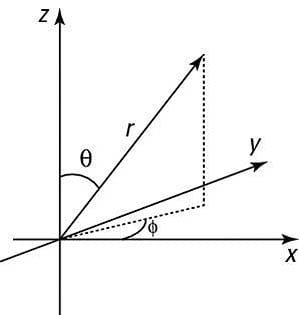
In the spherical coordinate system, you locate points with a radius vector named r, which has three components: