When a particle doesn't have as much energy as the potential of a barrier, you can use the Schrödinger equation to find the probability that the particle will tunnel through the barrier's potential. You can also find the reflection and transmission coefficients, R and T, as well as calculate the transmission coefficient using the Wentzel-Kramers-Brillouin (WKB) approximation.
Here's how it works: When a particle doesn't have as much energy as the potential of the barrier, you're facing the situation shown in the following figure.
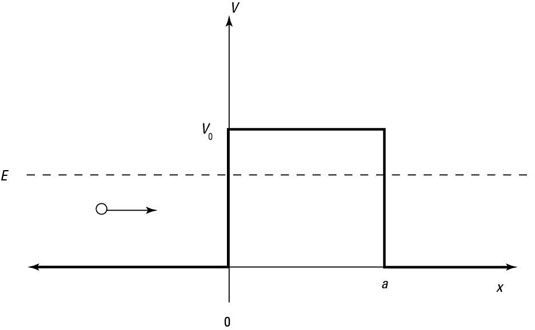
In this case, the Schrödinger equation looks like this:


All this means that the solutions for
![]()
are the following:

This situation is similar to the case where E > V0, except for the region
![]()
The wave function oscillates in the regions where it has positive energy, x x > a, but is a decaying exponential in the region
![]()
You can see what the probability density,
![]()
looks like in the following figure.

How to find the reflection and transmission coefficients
How about the reflection and transmission coefficients, R and T? Here's what they equal:

As you may expect, you use the continuity conditions to determine A, B, and F:

A fair bit of algebra and trig is involved in solving for R and T; here's what R and T turn out to be:

Despite the equation's complexity, it's amazing that the expression for T can be nonzero. Classically, particles can't enter the forbidden zone
![]()
because E 0, where V0 is the potential in that region; they just don't have enough energy to make it into that area.
How particles tunnel through regions
Quantum mechanically, the phenomenon where particles can get through regions that they're classically forbidden to enter is called tunneling. Tunneling is possible because in quantum mechanics, particles show wave properties.
Tunneling is one of the most exciting results of quantum physics — it means that particles can actually get through classically forbidden regions because of the spread in their wave functions. This is, of course, a microscopic effect — don't try to walk through any closed doors — but it's a significant one. Among other effects, tunneling makes transistors and integrated circuits possible.
You can calculate the transmission coefficient, which tells you the probability that a particle gets through, given a certain incident intensity, when tunneling is involved. Doing so is relatively easy in the above example because the barrier that the particle has to get through is a square barrier. But in general, calculating the transmission coefficient isn't so easy. Read on.
How to find the transmission coefficient with the WKB approximation
The way you generally calculate the transmission coefficient is to break up the potential you're working with into a succession of square barriers and to sum them. That's called the Wentzel-Kramers-Brillouin (WKB) approximation — treating a general potential, V(x), as a sum of square potential barriers.
The result of the WKB approximation is that the transmission coefficient for an arbitrary potential, V(x), for a particle of mass m and energy E is given by this expression (that is, as long as V(x) is a smooth, slowly varying function):

In this equation
![]()
So now you can amaze your friends by calculating the probability that a particle will tunnel through an arbitrary potential. It's the stuff science fiction is made of — well, on the microscopic scale, anyway.





