While analyzing the equations of string theory, some physicists realized that the ends of open strings didn’t just hover out in empty space. Instead, it was as if the end of the open string was attached to an object, but string theory at the time didn’t have objects (other than strings) for it to attach to.
The motivation for D-branes came from work by Joe Polchinski, Jin Dai, and Rob Leigh of the University of Texas, and independent work performed at the same time by Czech physicist Petr Hořava.
To solve this problem, the physicists introduced the D-brane, a surface that exists within the 10-dimensional superstring theory so open strings can attach to them. These branes, and the strings attached to them, are shown in the figure.
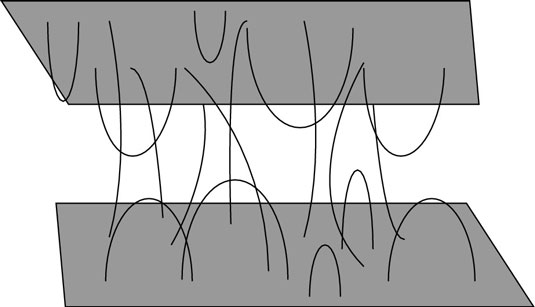
The “D” in D-brane comes from Johann Peter Gustav Lejeune Dirichlet, a German mathematician whose relationship to the D-brane comes from a special type of boundary condition, called the Dirichlet boundary condition, which the D-branes exhibit.
It’s easiest to visualize these branes as flat planes, but the D-branes can exist in any number of dimensions from zero to nine, depending on the theory. A 5-dimensional D-brane would be called a D5-brane. It’s easy to see how quickly these D-branes can multiply.
You could have a D5-brane intersecting a D3-brane, which has a D1-brane extending off of it. Open superstrings could have one end on the D1-brane and the other end on the D5-brane, or on some other D5-brane in another position, and D9-branes (extended in all nine dimensions of space-time) could be in the background of all of them.
At this point, it’s clear that it begins to be quite difficult to picture this 10-dimensional space or keep all the possible configurations straight in any meaningful way.
In addition, the D-branes can be either finite or infinite in size. Scientists honestly don’t know the real limitations of how these branes behave. Prior to 1995, few people paid much attention to them.

