According to the laws of physics, the force of friction, Ffriction, always acts to oppose the force you apply when you try to move an object. Friction is proportional to the force with which an object pushes against the surface you’re trying to slide it along.
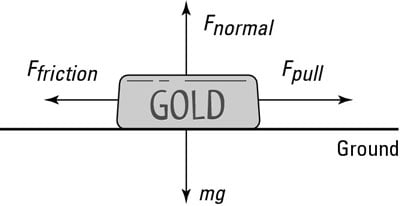
As you can see in the figure, the force with which the gold ingot presses against the ground in this situation is just its weight, or mg. The ground presses back with the same force in accordance with Newton’s third law.
Newton’s third law of motion is famous, especially in wrestling and drivers’ ed circles, but you may not recognize it in all its physics glory: “Whenever one body exerts a force on a second body, the second body exerts an oppositely directed force of equal magnitude on the first body.” The more popular version of this is “For every action, there’s an equal and opposite reaction.” But for physics, it’s better to express the originally intended version, in terms of forces, not actions.
The force that pushes up against the ingot, perpendicular to the surface, is called the normal force, and its symbol is N. The normal force isn’t necessarily equal to the force due to gravity; it’s the force perpendicular to the surface an object is sliding on. In other words, the normal force is the force pushing the two surfaces together, and the stronger the normal force, the stronger the force due to friction.
In the case of the figure, because the ingot slides along the horizontal ground and is pulled by a force that is parallel to the ground, the normal force has the same magnitude as the weight of the ingot, so Fnormal = mg. You have the normal force, which is the force pressing the ingot and the ground together.

