Simple Error Propagation Formulas for Simple Expressions

Even though some general error-propagation formulas are very complicated, the rules for propagating SEs through some simple mathematical expressions are much easier to work with. Here are some of the most common simple rules.

All the rules that involve two or more variables assume that those variables have been measured independently; they shouldn't be applied when the two variables have been calculated from the same raw data.

Adding or subtracting a constant doesn't change the SE

Adding (or subtracting) an exactly known numerical constant (that has no SE at all) doesn't affect the SE of a number. So if x = 38 ± 2, then x + 100 = 138 ± 2. Likewise, if x = 38 ± 2, then x – 15 = 23 ± 2.

Multiplying (or dividing) by a constant multiplies (or divides) the SE by the same amount

Multiplying a number by an exactly known constant multiplies the SE by that same constant. This situation arises when converting units of measure. For example, to convert a length from meters to centimeters, you multiply by exactly 100, so a length of an exercise track that's measured as 150 ± 1 meters can also be expressed as 15,000 ± 100 centimeters.

For sums and differences: Add the squares of SEs together

When adding or subtracting two independently measured numbers, you square each SE, then add the squares, and then take the square root of the sum, like this:

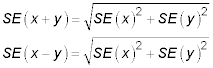
For example, if each of two measurements has an SE of ± 1, and those numbers are added together (or subtracted), the resulting sum (or difference) has an SE of

A useful rule to remember is that the SE of the sum or difference of two equally precise numbers is about 40 percent larger than the SE of one of the numbers.

When two numbers of different precision are combined (added or subtracted), the precision of the result is determined mainly by the less precise number (the one with the larger SE). If one number has an SE of ± 1 and another has an SE of ± 5, the SE of the sum or difference of these two numbers is

or only slightly larger than the larger of the two individual SEs.

For averages: The square root law takes over

The SE of the average of N equally precise numbers is equal to the SE of the individual numbers divided by the square root of N.

For example, if your lab analyzer can determine a blood glucose value with an SE of ± 5 milligrams per deciliter (mg/dL), then if you split up a blood sample into four specimens, run them through the analyzer, and average the four results, the average will have an SE of

The average of four numbers is twice as precise as (has one-half the SE of) each individual number.

For products and ratios: Squares of relative SEs are added together

The rule for products and ratios is similar to the rule for adding or subtracting two numbers, except that you have to work with the relative SE instead of the SE itself. The relative SE of x is the SE of x divided by the value of x.

So, a measured weight of 50 kilograms with an SE of 2 kilograms has a relative SE of 2/50, which is 0.04 or 4 percent. When multiplying or dividing two numbers, square the relative standard errors, add the squares together, and then take the square root of the sum. This gives you the relative SE of the product (or ratio). The formulas are

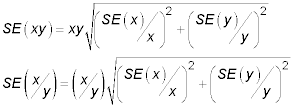
This formula may look complicated, but it's actually very easy to use if you work with percent errors (relative precision). Then it works just like the "add the squares" rule for addition and subtraction. So if one number is known to have a relative precision of ± 2 percent, and another number has a relative precision of ± 3 percent, the product or ratio of these two numbers has a relative precision (in percentage) of

Note that multiplying a number by an exactly known constant doesn't change the relative SE. For example, doubling a number represented by x would double its SE, but the relative error (SE/x) would remain the same because both the numerator and the denominator would be doubled.

For powers and roots: Multiply the relative SE by the power

For powers and roots, you have to work with relative SEs. When x is raised to any power k, the relative SE of x is multiplied by k; and when taking the kth root of a number, the SE is divided by k. So squaring a number (raising it to the power of 2) doubles its relative SE, and taking the square root of a number (raising it to the power of ½) cuts the relative SE in half. Another important special case of the power rule is that the relative error of the reciprocal of a number (raising it to the power of -1) is the same as the relative error of the number itself.

For example, because the area of a circle is proportional to the square of its diameter, if you know the diameter with a relative precision of ± 5 percent, you know the area with a relative precision of ± 10 percent.For example, under certain assumptions, the half-life (t_1/2) of a drug in the body is related to the terminal elimination rate constant (k_e) for the drug by the formula: t_1/2 = 0.693/k_e. A pharmacokinetic regression analysis might produce the result that k_e = 0.1633 ± 0.01644 (k_e has units of "per hour"). You can calculate that t_1/2 = 0.693/0.1633 = 4.244 hours.

How precise is this half-life value? First you calculate the relative SE of the k_e value as SE(k_e )/k_e, which is 0.01644/0.1633 = 0.1007, or about 10 percent.

Because k_e has a relative precision of ± 10 percent, t_1/2 also has a relative precision of ± 10 percent, because t_1/2 is proportional to the reciprocal of k_e (you can ignore the 0.693 entirely, because relative errors are not affected by multiplying or dividing by a known constant).

If the t_1/2 value of 4.244 hours has a relative precision of 10 percent, then the SE of t_1/2 must be 0.4244 hours, and you report the half-life as 4.24 ± 0.42 hours.