When trigonometry quadratic equations factor, life is good. When they don’t, you can still survive, thanks to that wonderful quadratic formula. In case you’ve forgotten the exact formula, here it is.
The quadratic formula says that if you have a quadratic equation in the form ax2 + bx + c = 0, where a is not 0, then its solutions are
In trigonometry, a trig function replaces the x or variable part of the quadratic formula. For example, find the solution of sin2 x – 4sin x – 1 = 0 for all angles between 0 and 360 degrees. Instead of just x’s, the variable terms are sin x’s.
Identify the values of the a, b, and c in the formula.
The values are a = 1, b = –4, and c = –1.
Fill in the quadratic formula with these values and simplify.
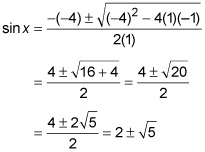
Find approximate values for sin x from the solved form.
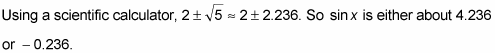
Use a table of values to find approximate angles with these sines.
If sin x = 4.236, you get an impossible result. The value of the sine ranges from –1 to 1, so sin x can’t have this value.
If sin x = –0.236, then x = sin–1(–0.236) ≈ –14º or 346º. These are the same angle. First, you write it as a negative angle and then as its positive equivalent.
Another angle satisfies this equation, too. The other negative angle that has a 14-degree reference angle is the third-quadrant angle of 194 degrees.

