Some of the more-advanced graphing calculators make short work of solving trigonometry equations. A graphing calculator comes in very handy when the equation is complicated, has several different functions or angle multiples, or has fractional or decimal values that don’t lend themselves to traditional solving methods. For example, you may prefer to use a graphing calculator to solve equations like cos 2x = 2cos x and cos2 x – 0.4sin x = 0.6.
First, here’s how to solve cos 2x = 2cos x for all solutions between –2π and 2π.
Put the expression on the left side of the equation in the y menu (the graphing menu) of your calculator. Put the expression on the right as a second entry. (Be sure your calculator is set in the radian mode.)
y1 = cos 2x
y2 = 2cos x
Set the window of your calculator to show the graphs.
Set the x values from –2π to 2π. In decimal form, let x = –6.5 to 6.5 to give a little room on either side of the left and right ends.
Set the y values to go from –3 to 3. Doing so gives room above and below the graph. If you have an auto fit capability, use it to make the graph fit automatically after you choose the x values you want the graph to encompass.
Graph the two functions, and see where they intersect (see the following figure).
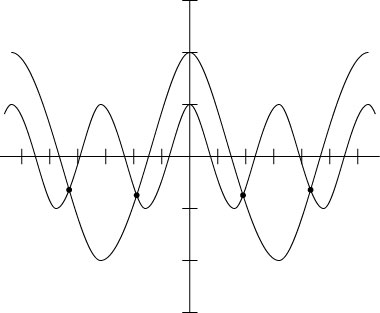 The graphs of y = cos 2x and y = 2cos x.
The graphs of y = cos 2x and y = 2cos x.Use the intersect feature on the calculator to determine the solutions.
The x-coordinates of the intersection points are the solutions (rounded to four decimal places): x = –4.3377, –1.9455, 1.9455, and 4.3377. These solutions are in radians — the π value is already multiplied through.
You can also find the solutions to the above example with a graphing calculator’s solver feature, but usually, you still need to look at the graph anyway so you know how many solutions you’re trying to find. The solver feature usually finds only one solution at a time, and you need a hint to know where to find them.
This next example has decimals built in, so you probably can’t factor it. You can solve it by using identities and writing it as a quadratic, and then using the quadratic formula. This calculator method gives you another option.
Solve cos2 x – 0.4sin x = 0.6 for all angles between –π and π.
Put the expression on the left in the graphing y menu of your calculator. Put the expression on the right as a second entry. (Be sure your calculator is set in the radian mode.)
y1 = cos2 x – 0.4sin x
y2 = 0.6
Set the window of your calculator to show the graphs.
Set the horizontal, x values from –π to π. In decimal form, use x = –3.2 to 3.2 to give a little room on either side of the ends.
Set the vertical, y values to go from –3 to 3. Doing so gives room above and below the graph. If you have an auto fit capability, use it to make the graph fit automatically.
Graph the two functions, and see where they intersect (see the following figure).
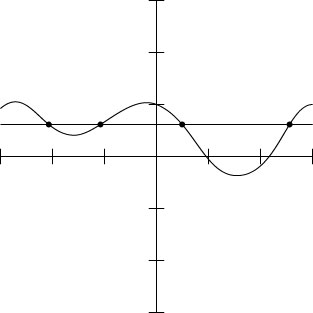 The graphs of y = cos2 x – 0.4sin x and y = 0.6.
The graphs of y = cos2 x – 0.4sin x and y = 0.6.Use the intersect feature on the calculator to determine the solutions.
The x-coordinates of the intersection points are the solutions (rounded to four decimal places): x = –2.0998, –1.0418, 0.4817, and 2.6598. These solutions are in radians — the π value is already multiplied through.

