Land surveyors use trigonometry and their fancy equipment to measure things like the slope of a piece of land (how far it drops over a certain distance). Have you ever noticed a worker along the road, peering through an instrument, looking at a fellow worker holding up a sign or a flag?
Haven't you ever wondered what they're doing? Have you wanted to get out and look through the instrument, too? With trigonometry, you can do just what those workers do — measure distances and angles.
You may recognize that the slope of land downward is sort of like an angle of depression. Slopes, angles of depression, and angles of elevation are all interrelated because they use the same trig functions. It's just that in slope applications, you're solving for the angle rather than a length or distance.
To solve one of these surveying problems involving slope, you can use the trig ratios and right triangles. One side of the triangle is the distance from one worker to the other; the other side is the vertical distance from the ground to a point on a pole. You form a ratio with those measures and determine the angle — voilà!
Suppose that Elliott and Fred are making measurements for the road-paving crew. They need to know how much the land slopes downward along a particular stretch of road to be sure there's proper drainage.
Elliott walks 80 feet from Fred and holds up a long pole, perpendicular to the ground, that has markings every inch along it. Fred looks at the pole through a sighting instrument. Looking straight across, parallel to the horizon, Fred sights a point on the pole 50 inches above the ground — call it point A. Then Fred looks through the instrument at the bottom of the pole, creating an angle of depression.
What is the angle of depression, or slope of the road, to where Elliott is standing?
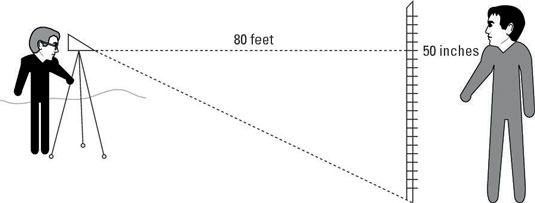
Identify the parts of the right triangle that you can use to solve the problem.
The values you know are for the sides adjacent to and opposite the angle of depression. Call the angle measure x.
Determine which trig function to use.
The tangent of the angle with measure x uses opposite divided by adjacent.
Write an equation with the trig function; then insert the values that you know.
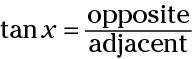
In this problem, you need to write the equation with a common unit of measurement — either feet or inches. Changing 80 feet to inches makes for a big number; changing 50 inches to feet involves a fraction or decimal. Whichever unit you choose is up to you. In this example, convert feet to inches.
80 feet = 80 x 12 inches = 960 inches
Substituting in the values, you get the tangent of some angle with a measure of x degrees:
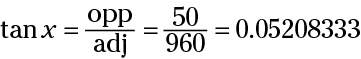
Solve for the value ofx.
In the Appendix, you see that an angle of 2.9 degrees has a tangent of 0.0507, and a 3-degree angle has a tangent of 0.0524. The 3-degree angle has a tangent that's closer to 0.05208333, so you can estimate that the road slopes at a 3-degree angle between Elliott and Fred.
Another way to solve for that angle measure is to use a scientific calculator and the inverse tangent function. Your calculator says that the angle whose tangent is 0.05208333 is an angle of 2.98146 degrees. So, the estimate of three degrees from the table is right on.

