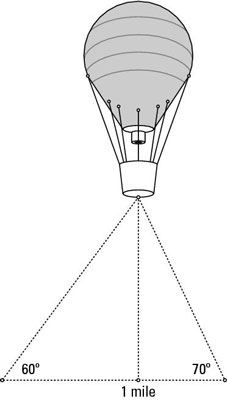
You can use trigonometry functions to determine the altitude of a balloon. Cindy and Mindy, standing a mile apart, spot a hot-air balloon directly above a particular point on the ground somewhere between them. The angle of elevation from Cindy to the balloon is 60 degrees; the angle of elevation from Mindy to the balloon is 70 degrees. How high is the balloon?
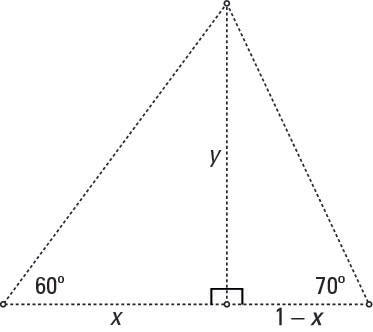
You see that two right triangles are formed. The two triangles share a side — the one opposite the measured acute angle in each. Call the length of that shared side y. The two adjacent sides add up to 1 mile, so you can keep the variables to a minimum by naming one side x and the other 1 – x.
To figure out how high the balloon is, follow these steps:
Identify the parts of the triangles that you can use to solve the problem.
In both triangles, you have variables for the adjacent and opposite sides of the acute angles of elevation.
Determine which trig function to use.
The tangent ratio uses the opposite and adjacent sides.
Write equations with the trig functions.
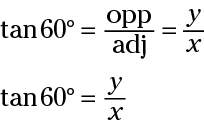
and
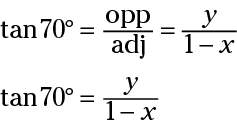
Solve forxby setting the equations equal to one another.
First solve each of the equations for y.
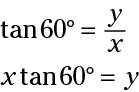
and
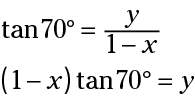
Set those two equations equal to one another and solve for x.
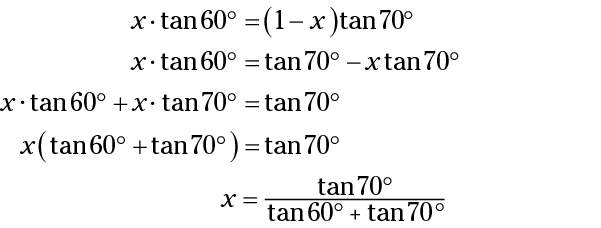
Solve for the value ofx.
You find the value of x by finding the values of the functions with a calculator or in the Appendix. Upon doing so, you find that x is approximately 0.613 miles. Put that value into one of the equations to solve for y:
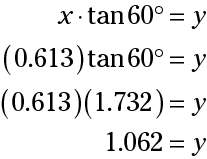
The balloon is 1.062 miles high — sounds a tad high!

