To graph the secant curve, you first identify the asymptotes by determining where the reciprocal of secant — cosine — is equal to 0. Then you sketch in that reciprocal, so you can determine the turning points and general shape of the secant graph.
Determining the asymptotes of a secant function
Because the secant equals 1 divided by the cosine, the secant function is undefined, or doesn’t exist, whenever the cosine function is equal to 0. You can write the equations of the asymptotes by setting y equal to those values where the cosine is equal to 0, so the asymptotes are
and so on. Another way to express the equations of all the asymptotes is to write
Sketching the graph of a secant function
Using the graph of the cosine to sketch the graph of the secant function is the easiest method. Graph the cosine very lightly or with a dotted curve — and then do the same with the asymptotes. A lot of busywork is associated with this graph, but you just have to ignore all the extra stuff and zoom in on the graph that you want. To sketch the graph of the secant function, follow these steps:
Sketch the graph of y = cos x from –4π to 4π, as shown in the following figure.
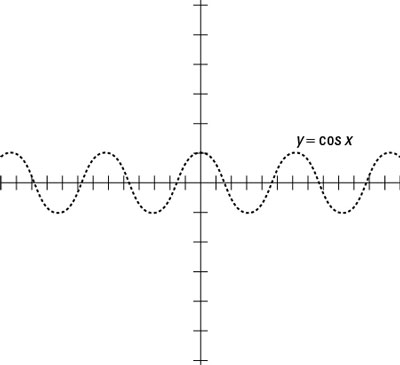A sketch of the cosine function.Draw the vertical asymptotes through the x-intercepts (where the curve crosses the x-axis), as the next figure shows.
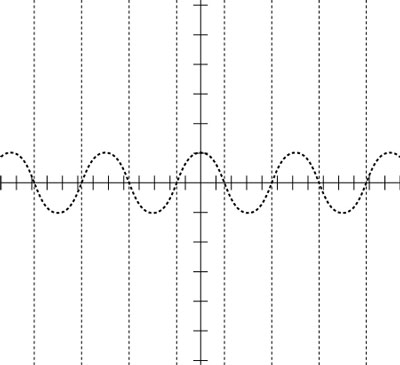The vertical asymptotes of secant drawn on the graph of cosine.Draw y = sec x between the asymptotes and down to (and up to) the cosine curve, as shown in this figure.
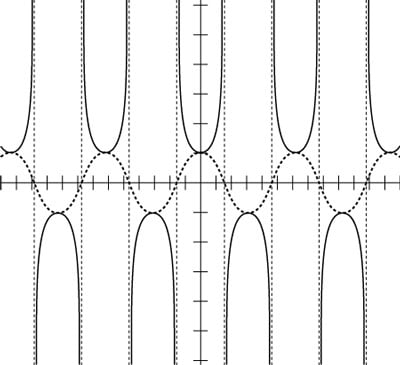Drawing the secant curve by using the cosine as a guide.The secant goes down to the top of the cosine curve and up to the bottom of the cosine curve.
