-
The slope of a line is the change in Y over the change in X. For example, a slope of
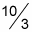
means as the x-value increases (moves right) by 3 units, the y-value moves up by 10 units on average.
-
The y-intercept is the value on the y-axis where the line crosses. For example, in the equation y=2x – 6, the line crosses the y-axis at the value b= –6. The coordinates of this point are (0, –6); when a line crosses the y-axis, the x-value is always 0.
To save a great deal of time calculating the best fitting line, first find the “big five,” five summary statistics that you’ll need in your calculations:
-
The mean of the x values

-
The mean of the y values

-
The standard deviation of the x values (denoted sx)
-
The standard deviation of the y values (denoted sy)
-
The correlation between X and Y (denoted r)
Finding the slope of a regression line
The formula for the slope, m, of the best-fitting line is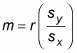
where r is the correlation between X and Y, and sx and sy are the standard deviations of the x-values and the y-values, respectively. You simply divide sy by sx and multiply the result by r.
Note that the slope of the best-fitting line can be a negative number because the correlation can be a negative number. A negative slope indicates that the line is going downhill. For example, if an increase in community center programs is related to a decrease in the number of crimes in a linear fashion; then the correlation and hence the slope of the best-fitting line is negative in this case.
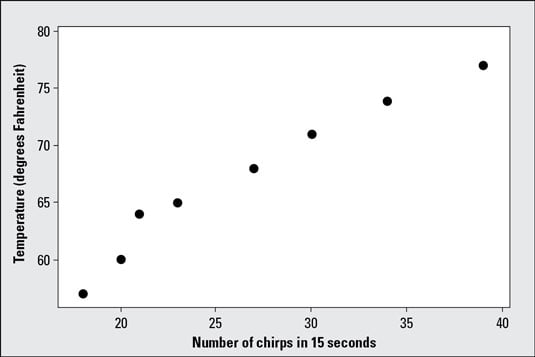
The correlation and the slope of the best-fitting line are not the same. The formula for slope takes the correlation (a unitless measurement) and attaches units to it. Think of sy divided by sx as the variation (resembling change) in Y over the variation in X, in units of X and Y. For example, variation in temperature (degrees Fahrenheit) over the variation in number of cricket chirps (in 15 seconds).
Finding the y-intercept of a regression line
The formula for the y-intercept, b, of the best-fitting line is b = y̅ -mx̅, where x̅ and y̅ are the means of the x-values and the y-values, respectively, and m is the slope.So to calculate the y-intercept, b, of the best-fitting line, you start by finding the slope, m, of the best-fitting line using the above steps. Then to find the y-intercept, you multiply m by x̅ and subtract your result from y̅.
Always calculate the slope before the y-intercept. The formula for the y-intercept contains the slope!

