The relationship between margin of error and sample size is simple: As the sample size increases, the margin of error decreases. This relationship is called an inverse because the two move in opposite directions. If you think about it, it makes sense that the more information you have, the more accurate your results are going to be (in other words, the smaller your margin of error will get). (That assumes, of course, that the data were collected and handled properly.)
A simple example
Suppose that the Gallup Organization’s latest poll sampled 1,000 people from the United States, and the results show that 520 people (52%) think the president is doing a good job, compared to 48% who don’t think so. First, assume you want a 95% level of confidence, so you find z* using the following table.| z*-Values for Selected (Percentage) Confidence Levels | |
| Percentage Confidence | z*-Value |
|---|---|
| 80 | 1.28 |
| 90 | 1.645 |
| 95 | 1.96 |
| 98 | 2.33 |
| 99 | 2.58 |
The number of Americans in the sample who said they approve of the president was found to be 520. This means that the sample proportion,
is 520 / 1,000 = 0.52. (The sample size, n, was 1,000.) The margin of error for this polling question is calculated in the following way:
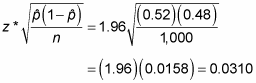
According to this data, you conclude with 95% confidence that 52% of all Americans approve of the president, plus or minus 3.1%.
Using the same formula, you can look at how the margin of error changes dramatically for samples of different sizes. Suppose in the presidential approval poll that n was 500 instead of 1,000. Now the margin of error for 95% confidence is
which is equivalent to 4.38%. If n is increased to 1,500, the margin of error (with the same level of confidence) becomes
or 2.53%. Finally, when n = 2,000, the margin of error is
or 2.19%.

