In algebra, simplifying and factoring expressions are opposite processes. Simplifying an expression often means removing a pair of parentheses; factoring an expression often means applying them.
Suppose you begin with the expression 5x(2x2 – 3x + 7). To simplify this expression, you remove the parentheses by multiplying 5x by each of the three terms inside the parentheses:
= 10x3 – 15x2 + 35x
You can factor the resulting expression by replacing the parentheses: Simply divide each term by a factor of 5x:
5x(2x2 – 3x + 7)
The two forms of this expression — 5x(2x2 – 3x + 7) and 10x2 – 15x2 + 35x — are equivalent. Neither form is better than the other. But, depending upon the circumstances, one form may be more useful.
Simplifying messy expressions
You can use simplifying to clean up messy expressions and make them easier to work with. Suppose you're working with the following expression:
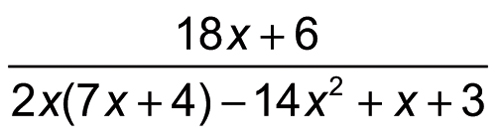
To clean it up, begin by simplifying the denominator:
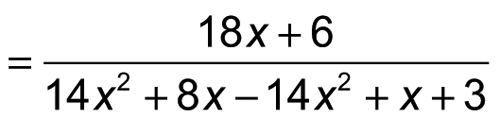
Then you combine like terms in the denominator; notice that the x2 terms cancel each other out.
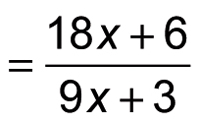
This fraction looks a lot simpler, but you can simplify even further by factoring both the numerator and denominator:
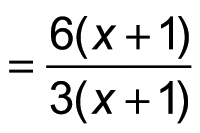
Now you can cancel a factor of x + 1 and simplify the resulting fraction as follows:
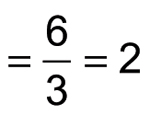
Through a combination of simplifying and factoring, the complicated-looking expression turns out to be a very simple constant!
Factoring quadratic polynomials
Factoring can be tricky, especially when you need to factor a polynomial with large coefficients, such as 15x2 + 47 – 10. Here's an easy way to factor quadratic polynomials of the form ax2 + bx + c:
Begin by drawing a large X, placing the value ac in the top quadrant and b in the bottom quadrant.
Suppose you want to factor the polynomial 6x2 + 11x + 4. Note that in this polynomial, a = 6, b = 11, and c = 4. In this problem, ac = 6×4 = 24 and b = 11.

Find a pair of numbers that multiply to the top number and add to the bottom number, and place these in the two side quadrants (the order doesn't matter).
For the example, you want to find a pair of numbers that multiplies to 24 and adds up to 14. Begin by listing all the factor pairs of 24: 1×24, 2×12, 3×8, and 4×6. Notice that 3 + 8 = 11, so this is the correct pair of numbers.

Make two fractions using ax for the numerator and the two numbers you placed in the side quadrants as denominators.
Here, the value ax = 6x, and the numbers in the two side quadrants are 3 and 8:

Reduce these two fractions to lowest terms (keeping the results with both a numerator and denominator).

To finish, add the numerator and denominator of each fraction to find the two factors of the original polynomial.

Therefore, 6x2 + 11 + 4 = (2x + 1)(3x + 4)
Now, try the same method on the more difficult polynomial 15x2 + 47x – 10. In this case, a = 15, b = 47, and c = –10.
Begin by drawing a large X, placing the value ac in the top quadrant and b in the bottom quadrant.
In this problem, ac = 15 × –10 = –150 and b = 47.

Find a pair of numbers that multiply to the top number and add to the bottom number, and place these in the two side quadrants (the order doesn't matter).
You're looking for a pair of numbers that multiply to –150, so one number is positive and the other is negative. And these two numbers also add up to 47, so the positive number is the "bigger" of the two numbers.
So, here are the factor pairs that work: –1×150, –2×75, –3×50, –5×30, –6×25, and –10×15. Notice that –3 + 50 = 47, so this is the correct pair of numbers.

Make two fractions using ax for the numerator and the two numbers you placed in the side quadrants as denominators.
Here, the value ax = 15x, and the numbers in the two side quadrants are –3 and 50:

Reduce these two fractions to lowest terms (keeping the results with both a numerator and denominator).

To finish, add the numerator and denominator of each fraction to find the two factors of the original polynomial.

Therefore, 15x2 + 47x – 10= (5x – 1)(3x + 10).





