For the numeracy curriculum you mainly need to know about road maps. For example, you may need to find the shortest route between two towns along two different roads – you find the distance of each route and see which is shorter.
Scales and distance
One of the most important things to know about a map is its scale. This ratio tells you the relationship between distances depicted on the map and distances in reality.If a map has a scale of 1:100,000, it means that 1 centimetre on the map represents 100,000 centimetres (the same as 1 kilometre) in real life. The scale allows you to say how big a real-life object is if you know how big its picture is on the map, as well as how big something should be on the map if you know its size in real life.
The most common map-based questions involve solving this type of problem. The exam question may show you a map and ask you to do some measuring, or the question may just give you the scale and a distance (either on the map or in real life) and ask you to work out the other distance.The key to doing scales sums is to remember that multiplying by numbers bigger than one makes things bigger and dividing by numbers bigger than one makes things smaller. Here are the steps to do a sum involving a ‘one to lots’ scale, starting from a distance on the map:
-
If you don’t know the distance on the map, measure the distance on the map.
Write down the distance you measure, giving the right units – normally centimetres.
-
Times the map distance by the scale.
-
Convert your big number into more appropriate units.
If you’re working in centimetres, divide by 100 to get metres. If you need an answer in kilometres, divide the number of metres by 1,000. The number is your answer.
The best-laid plans
A slight variant on a map is a plan. The only real difference is one of size: a map tends to show how to navigate fairly large areas and a plan shows the general layout of something smaller.You can often deal with plans in the same way you play with compound rectangles. For example, you may need to find the perimeter or the area of the shape of the plan.
When you work with a scale, always convert your measurements from map distances to real-life distances before you start doing the shape sums – especially when you work with area.
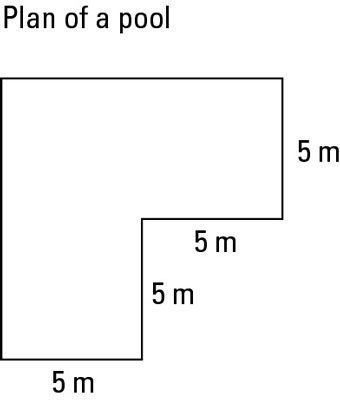
A plan is supposed to be a way of simplifying complicated shapes so you can understand the layout of, say, a room. Unfortunately, this description doesn’t seem to have reached maths examiners, so they persist in giving you plans that look like an explosion at the bingo hall – numbers everywhere and a load of annoyed people trying not to trip up.In an exam question, you probably won’t need to measure the plan but you do need to figure out what the question means. Here are a few pointers:
-
Width and length: If you need to find the width or length of a shape, check whether the plan already shows the measurement – if you see an arrow that goes all the way across or all the way along the shape, the number on that arrow is your width or length.
If not, you probably need to add up the component parts: find a series of arrows that go all the way across or along the shape and add them up.
-
Perimeter: To find the perimeter, you need to add up all of the lengths around the edge of the shape. If any of the lengths are missing, find them by taking away the appropriate arrows from the full length.
If the perimeter has gaps, like a fence with gates, you can either leave the gaps out as you add up, or work out the whole perimeter and then take away the gaps at the end.
-
Area: To find the area of a plan, split up the shape into simpler shapes and add up the area of each shape. The total area is the sum of all the other areas. Make sure you use the same units throughout.
-
Area of the walls: To work out the area of the walls, you need to work out the perimeter and times this by the height of the walls. If the walls contain doors or windows, you then need to take the area of these away from the total wall area.
-
Volume: To find a volume, such as how much water you can fit in a swimming pool, you find the area and then times it by the depth of the pool.
If this happens, don’t panic: you just divide the volume of the pool by the capacity of the bucket, or the area of the walls by the area each tin of paint covers.