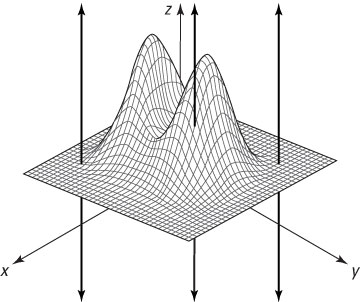
You can use a partial derivative to measure a rate of change in a coordinate direction in three dimensions. To do this, you visualize a function of two variables z = f(x, y) as a surface floating over the xy-plane of a 3-D Cartesian graph. The following figure contains a sample function.
Now take a look at the function z = y, shown here.
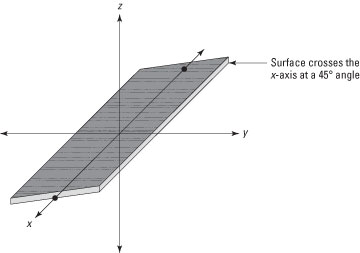
As you can see, this function looks a lot like the sloped roof of a house. Imagine yourself standing on this surface. When you walk parallel with the y-axis, your altitude either rises or falls. In other words, as the value of y changes, so does the value of z. But when you walk parallel with the x-axis, your altitude remains the same; changing the value of x has no effect on z.
So intuitively, you expect that the partial derivative
is 1. You also expect that the partial derivative
is 0.
Calculating partial derivatives isn’t much more difficult than evaluating regular derivatives. Given a function z(x, y), the two partial derivatives are
Here’s how you calculate them:
To calculate
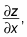
treat y as a constant and use x as your differentiation variable.
To calculate
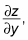
treat x as a constant and use y as your differentiation variable.
For example, suppose you’re given the equation z = 5x2y3. To find
treat y as if it were a constant — that is, treat the entire factor 5y3 as if it’s one big constant — and differentiate x2:
To find
treat x as if it were a constant — that is, treat 5x2 as if it’s the constant — and differentiate y3:
As another example, suppose that you’re given the equation z = 2ex sin y + ln x. To find
treat y as if it were a constant and differentiate by the variable x:
To find
treat x as if it were a constant and differentiate by the variable y:
As you can see, when differentiating by y, the ln x term is treated as a constant and drops away completely.
Returning to the earlier example — the “sloped-roof” function z = y — here are both partial derivatives of this function:
As you can see, this calculation produces the predicted results.

