Degrees aren’t the only way to measure angles. You can also use radians. Degrees and radians are just two different ways to measure angles, like inches and centimeters are two ways of measuring length.
The radian measure of an angle is the length of the arc along the circumference of the unit circle cut off by the angle. (But note that when you say that an angle has a measure of, say, 2 radians, you are talking about how wide the angle is opened (just like when you use degrees); you are not generally concerned about the length of the arc, even though that’s where the definition comes from.)
Look at the 30-degree angle in quadrant I of the figure below. Do you see the bolded section of the circle’s circumference that is cut off by that angle? Because a whole circle is 360 degrees, that 30-degree angle is one-twelfth of the circle. So the length of the bold arc is one-twelfth of the circle’s circumference.
Because the bold arc is one-twelfth of that, its length is ð/6, which is the radian measure of the 30-degree angle.
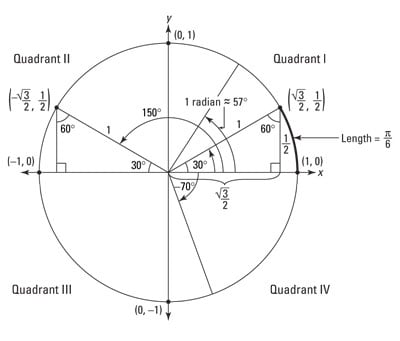
The unit circle’s circumference of 2ð makes it easy to remember that 360 degrees equals 2ð radians. Half the circumference has a length of ð, so 180 degrees equals ð radians.
If you focus on the fact that 180 degrees equals ð radians, other angles are easy:

The following list contains the formulas for converting from degrees to radians and vice versa.
To convert from degrees to radians:

To convert from radians to degrees:

In calculus, some problems use degrees and others use radians, but radians are the preferred unit. If a problem doesn’t specify the unit, do the problem in radians.

