You can integrate even powers of sines and cosines. For example, if you wanted to integrate sin2 x and cos2 x, you would use these two half-angle trigonometry identities:
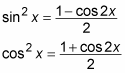
Here’s how you integrate cos2 x:
Use the half-angle identity for cosine to rewrite the integral in terms of cos 2x:
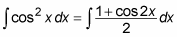
Use the Constant Multiple Rule to move the denominator outside the integral:
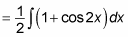
Distribute the function and use the Sum Rule to split it into several integrals:
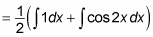
Evaluate the two integrals separately:
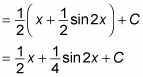
As a second example, here’s how you integrate sin2 x cos4 x:
Use the two half-angle identities to rewrite the integral in terms of cos 2x:
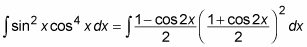
Use the Constant Multiple Rule to move the denominators outside the integral:
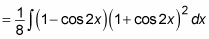
Distribute the function and use the Sum Rule to split it into several integrals:
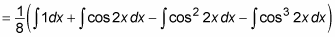
Evaluate the resulting odd-powered integrals:
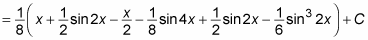
With the integration behind you, use algebra to simplify the result. To start, combine the first and third terms, and second and fifth terms:
Now distribute the result:

