Compositions of functions — that is, one function nested inside another — are of the form f(g(x)). You can integrate them by substituting u = g(x) when
You know how to integrate the outer function f.
The inner function g(x) differentiates to a constant — that is, it’s of the form ax or ax + b.
Here’s an example. Suppose that you want to integrate the function, csc2 (4x + 1).
This is a composition of two functions:
The outer function f is the csc2 (u) function.
The inner function is g(x) = 4x + 1, which differentiates to the constant 4.
The composition is held together by the equality u = 4x + 1. That is, the two basic functions f(u) = csc2 u and g(x) = 4x + 1 are composed by the equality u = 4x + 1 to produce the function f(g(x)) = csc2 (4x + 1).
Both criteria are met, so this integral is a prime candidate for substitution using u = 4x + 1. Here’s how you do it:
Declare a variable u and substitute it into the integral:
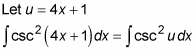
Differentiate u = 4x + 1 and isolate the x term.
This gives you the differential, du = 4dx.
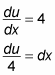
Substitute du/4 for dx in the integral:
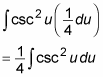
Evaluate the integral:
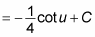
Substitute back 4x + 1 for u:
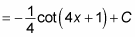
Here’s one more example. Suppose that you want to evaluate the following integral:
This is a composition of two functions:
The outer function f is a fraction — technically, an exponent of –1 — which you know how to integrate.
The inner function is g(x) = x – 3, which differentiates to 1.
The composition is held together by the equality u = x – 3. That is, the two basic functions
are composed by the equality u = x – 3 to produce the function
The criteria are met, so you can integrate by using the equality u = x – 3:
Declare a variable u and substitute it into the integral:
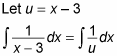
Differentiate u = x – 3 and isolate the x term.
This gives you the differential du = dx.
Substitute du for dx in the integral:
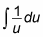
Evaluate the integral:
= ln |u| + C
Substitute back x – 3 for u:
= ln |x – 3| + C

