The parent graphs of tangent and cotangent are comparable because they both have asymptotes and x-intercepts. The only differences you can see are the values of theta where the asymptotes and x-intercepts occur. You can find the parent graph of the cotangent function f(x) = cot x,
by using the same techniques you use to find the tangent parent graph.
The table shows
so that you can see both the x-intercepts and the asymptotes in comparison. These points help you find the general shape of your graph so that you have a nice place to start.
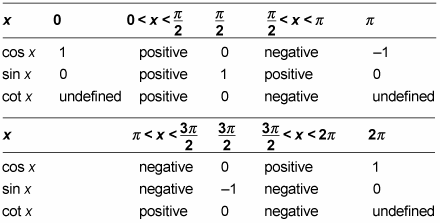
To sketch the full parent graph of cotangent, follow these steps:
Find the vertical asymptotes so you can find the domain.
Because cotangent is the quotient of cosine divided by sine, and
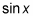
is sometimes 0, the graph of the cotangent function may have asymptotes, just like with tangent. However, these asymptotes occur whenever the

The cotangent parent graph repeats every pi units. Its domain is based on its vertical asymptotes: The first one comes at 0 and then repeats every pi radians. The domain, in other words, is
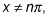
where n is an integer.
Find the values for the range.
Similar to the tangent function, you can define cotangent as
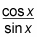
Both of these values can be decimals. The range of cotangent also has no restrictions; the ratios are any and all numbers,
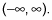
The closer you get to the values where
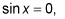
the smaller the number on the bottom of your fraction is and the larger the value of your overall fraction — in either the positive or negative direction.
Determine the x-intercepts.
The roots (or zeros) of cotangent occur wherever the cosine value is 0:
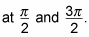
Evaluate what happens to the graph between the x-intercepts and the asymptotes.
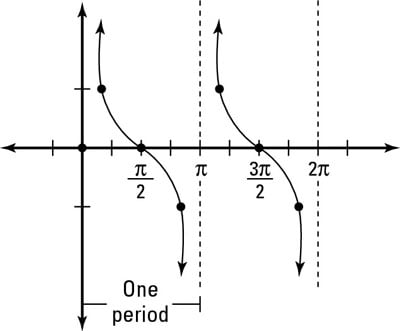
The positive and negative values in the four quadrants stay the same as in tangent, but the asymptotes change the graph. You can see the full parent graph of cotangent, cot x in the figure.

