If you know the first few terms of an arithmetic sequence, you can write a general expression for the sequence to find the nth term. To write the general expression, you must look for a pattern in the first few terms of the sequence, which demonstrates logical thinking (and we all want to be logical thinkers, right?). The formula you write must work for every integer value of n, starting with n = 1.
Sometimes this calculation is an easy task, and sometimes it's less apparent and more complicated. Sequences involving fractions and/or exponents tend to be more complicated and less obvious in their patterns. The easy ones to write include addition, subtraction, multiplication, or division by integers.
For example, to find the general formula for the nth term of the sequence 2/3, 3/5, 4/7, 5/9, 6/11, you should look at the numerator and the denominator separately:
The numerators begin with 2 and increase by one each time. This sequence is described by an = n + 1.
The denominators start with 3 and increase by two each time. This sequence is described by an = 2n + 1.
Therefore, this sequence can be expressed by this general formula:
To double check your formula and ensure that the answers work, plug in 1, 2, 3, and so on to make sure you get the original numbers from the given sequence.
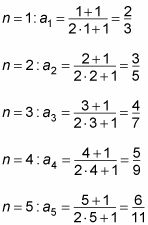
They all work, so you did it right!

