-
f(c) must be defined. The function must exist at an x value (c), which means you can't have a hole in the function (such as a 0 in the denominator).
-
The limit of the function as x approaches the value c must exist. The left and right limits must be the same; in other words, the function can't jump or have an asymptote. The mathematical way to say this is that
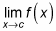
must exist.
-
The function's value at c and the limit as x approaches c must be the same.
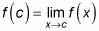
is continuous at x = 4 because of the following facts:
-
f(4) exists. You can substitute 4 into this function to get an answer: 8.
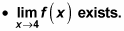
If you look at the function algebraically, it factors to this:
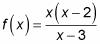
Nothing cancels, but you can still plug in 4 to get
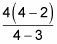
which is 8.
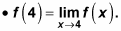
Both sides of the equation are 8, so f(x) is continuous at x = 4.
Functions that aren't continuous at an x value either have a removable discontinuity (a hole in the graph of the function) or a nonremovable discontinuity (such as a jump or an asymptote in the graph):
-
If the function factors and the bottom term cancels, the discontinuity at the x-value for which the denominator was zero is removable, so the graph has a hole in it.
For example, this function factors as shown:
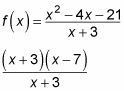
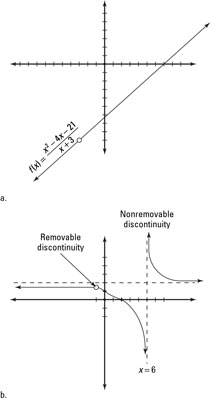
After canceling, it leaves you with x – 7. Therefore x + 3 = 0 (or x = –3) is a removable discontinuity — the graph has a hole, like you see in Figure a.
 The graph of a removable discontinuity leaves you feeling empty, whereas a graph of a nonremovable discontinuity leaves you feeling jumpy.
The graph of a removable discontinuity leaves you feeling empty, whereas a graph of a nonremovable discontinuity leaves you feeling jumpy. -
If a term doesn't cancel, the discontinuity at this x value corresponding to this term for which the denominator is zero is nonremovable, and the graph has a vertical asymptote.
The following function factors as shown:
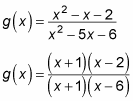
Because the x + 1 cancels, you have a removable discontinuity at x = –1 (you'd see a hole in the graph there, not an asymptote). But the x – 6 didn't cancel in the denominator, so you have a nonremovable discontinuity at x = 6. This discontinuity creates a vertical asymptote in the graph at x = 6. Figure b shows the graph of g(x).

